题目内容
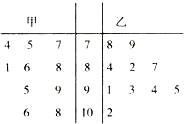某次考试中，从甲、乙两个班各随机抽取10名学生的成绩进行统计分析，学生成绩的茎叶图如图所示，成绩不小于90分为及格．（Ⅰ）从每班抽取的学生中各随机抽取一人，求至少有一人及格的概率
（Ⅱ）从甲班10人中随机抽取一人，乙班10人中随机抽取两人，三人中及格人数记为X，求X的分布列和期望．
考点：离散型随机变量的期望与方差,茎叶图
专题：概率与统计
分析：（Ⅰ）由茎叶图可知：甲班有4人及格，乙班有5人及格，由此利用对立事件概率计算公式能求出至少有一人及格的概率．
（Ⅱ）由题意知X的所有可能取值为0，1，2，3，分别求出相应的概率，由此能求出X的分布列和期望．
（Ⅱ）由题意知X的所有可能取值为0，1，2，3，分别求出相应的概率，由此能求出X的分布列和期望．
解答：
解：（Ⅰ）由茎叶图可知：甲班有4人及格，乙班有5人及格，
设事件“从每班10名同学中各抽取一人，至少有一人及格”为事件A．
则P（
）=
=
，
所以P（A）=1-P（
）=
．…（4分）
（Ⅱ）由题意可知X的所有可能取值为0，1，2，3．…（5分）
P（X=0）=
=
，
P（X=1）=
+
=
，
P（X=2）=
+
=
，
P（X=3）=
=
．…（9分）
所以X的分布列为
…（10分）
E（X）=0×
+1×
+2×
+3×
=
．…（12分）
设事件“从每班10名同学中各抽取一人，至少有一人及格”为事件A．
则P（
. |
| A |
| 6×5 |
| 10×10 |
| 3 |
| 10 |
所以P（A）=1-P（
. |
| A |
| 7 |
| 10 |
（Ⅱ）由题意可知X的所有可能取值为0，1，2，3．…（5分）
P（X=0）=
6
| ||
10
|
| 2 |
| 15 |
P（X=1）=
4
| ||
1
|
| 6×5×5 | ||
10
|
| 19 |
| 45 |
P（X=2）=
| 4×5×5 | ||
10
|
| ||
10
|
| 16 |
| 45 |
P（X=3）=
4
| ||
10
|
| 4 |
| 45 |
所以X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
E（X）=0×
| 2 |
| 15 |
| 19 |
| 45 |
| 16 |
| 45 |
| 4 |
| 45 |
| 7 |
| 5 |
点评：本题考查概率的求法，考查离散型随机变量的分布列和期望的求法，是中档题．
练习册系列答案
互动英语系列答案
相关题目
下列说法正确的是（ ）
| A、命题“若x2-5x+6=0，则x=2”的逆命题是“若x≠2，则x2-5x+6≠0” |
| B、命题“若x=2，则x2-5x+6=0”的否命题是“若x=2，则x2-5x+6≠0” |
| C、已知a，b∈R，则“a＞b”是“|a|＞|b|”的充要条件 |
| D、已知a，b∈R，则“ab≠0”是“a≠0”的充分条件 |
某学习小组在一次数学测验中，得100分的有1人，得95分的有1人，得90分的有2人，得85分的有4人，得80分和75分的各有1人，则该小组数学成绩的平均数、众数、中位数分别是（ ）
| A、85，85，85 |
| B、87，85，86 |
| C、87，85，85 |
| D、87，85，90 |
如图，在四棱锥P-ABCD中，四边形ABCD是矩形，侧面PAD⊥底面ABCD，若点E，F分别是PC，BD的中点．