题目内容
若0＜α＜2π，则使sinα＜
和cosα＞
同时成立的α的取值范围是（ ）
| ||
| 2 |
| 1 |
| 2 |
A、（-
| ||||
B、（0，
| ||||
C、（
| ||||
D、（0，
|
考点：三角函数线
专题：三角函数的图像与性质
分析：根据正弦函数和余弦函数的单调性分别求得在0＜α＜2π，满足已知条件α的范围，最后去交集即可．
解答：
解：∵0＜α＜2π，sinα＜
，
∴0＜α＜
或
＜α＜2π，①
∵0＜α＜2π，cosα＞
，
∴0＜α＜
，或
＜α＜2π，②
①②取交集得0＜α＜
或
＜α＜2π，
故选：D．
| ||
| 2 |
∴0＜α＜
| π |
| 3 |
| 2π |
| 3 |
∵0＜α＜2π，cosα＞
| 1 |
| 2 |
∴0＜α＜
| π |
| 3 |
| 5π |
| 3 |
①②取交集得0＜α＜
| π |
| 3 |
| 5π |
| 3 |
故选：D．
点评：本题主要考查了三角函数图象与性质，三角函数的单调性．解题可结合正弦函数和余弦函数的图象，可能更直观．
练习册系列答案
导学全程练创优训练系列答案
相关题目
函数y=ln（1-x）+
的定义域为（ ）
| x |
| A、{x|x≥0} |
| B、{x|x≤1} |
| C、{x|0＜x≤1} |
| D、{x|0≤x＜1} |
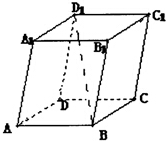
在平行六面体ABCD-A1B1C1D1中，用向量
，
，
来表示向量
为（ ）
| AB |
| AD |
| AA1 |
| BD1 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知f（x）是定义在R上的函数，满足f（x）+f（-x）=0，f（x-1）=f（x+1），当x∈[0，1），f（x）=
，函数f（x）的最小值为（ ）
| 2x |
| 4x+1 |
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
某学习小组在一次数学测验中，得100分的有1人，得95分的有1人，得90分的有2人，得85分的有4人，得80分和75分的各有1人，则该小组数学成绩的平均数、众数、中位数分别是（ ）
| A、85，85，85 |
| B、87，85，86 |
| C、87，85，85 |
| D、87，85，90 |
从1、2、3、4、5、6这六个数中，每次取出两个不同数记为a、b，则共可得到3
的不同数值的个数（ ）
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |