题目内容

在△ABC中，设h为∠A所对的边BC=a上的高，则三角形面积S△=
1
2
•a•h，由此类比：空间中，
 
．
考点：类比推理
专题：计算题,推理和证明
分析：三角形类比到空间三棱锥，根据面积类比体积，长度类比面积，可得结论．
解答： 解：三角形类比到空间三棱锥，根据面积类比体积，长度类比面积，可得：三棱锥ABCD中，三棱锥的体积为VA-BCD=
1
3
S△BCD•h．
故答案为：三棱锥ABCD中，三棱锥的体积为VA-BCD=
1
3
S△BCD•h．
点评：本题考查了类比推理，将平面中的性质类比到空间．
练习册系列答案
相关题目
若存在实数x使
3x+6
+
14-x
＞a成立，求常数a的取值范围
 
．
在a＞0，b＞0的条件下，三个结论：
①
2ab
a+b
≤
a+b
2
，
②
a+b
2
≤
a2+b2
2
，
③
b2
a
+
a2
b
≥a+b，
其中正确的序号是
 
．
由代数式的乘法法则类比推导向量的数量积的运算法则：
①m•n=n•m类比得到a•b=b•a；
②（m+n）•t=m•t+n•t类比得到（a+b）•c=a•c+b•c；
③（m•n）t=m（n•t） 类比得到（a•b）c=a（b•c）；
④t≠0，m•t=r•t⇒m=r类比得到p≠0，a•p=b•p⇒a=b；
⑤|m•n|=|m|•|n|类比得到|a•b|=|a|•|b|；
⑥
ac
bc
=
a
b
类比得到
a
•
c
b
•
c
=
a
b
．
以上式子中，类比得到的结论正确的序号是
 
．
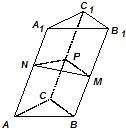类比正弦定理，如图，在三棱柱ABC-A1B1C1中，二面角B-AA1-C、C-BB1-A、B-CC1-A，所成的平面角分别为α、β、γ，则有
 
．
对于函数f（x）=x2（x＞0）图象上任意两点A（a，a2），B（b，b2），直线段AB必在曲线段AB的上方，则依据图象的特征可得不等式
a2+b2
2
＞（
a+b
2
）2（a＞0，b＞0），试分析函数y=lgx的图象特征，类比上述不等式可以得到
 
．
正方形ABCD的边长为1，则|
AB
+
AD
|为（　　）
A、1
B、
2
C、3
D、2
2
设
a
=（cosα，sinα），
b
=（cosα，1-
5
4sinα
），若
a
⊥
b
，则锐角α为（　　）
A、15°B、30°
C、45°D、60°
定义运算a?b=
a，a≥b
b，a＜b
，则函数y=1?lnx图象可能为（　　）
A、
B、
C、
D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网