题目内容
(文)已知函数f(x)是定义在R上且满足f(x)+f(-x)=0,f(x)+f(x+
)=0,且x∈(-
,0)时,f(x)=log
(1-x),则f(2010)+f(2011)=( )
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| A、1 | B、2 | C、-1 | D、-2 |
考点:抽象函数及其应用,函数的周期性
专题:函数的性质及应用
分析:由f(x)+f(-x)=0知,该函数是奇函数,所以f(0)=0,由f(x)+f(x+
)=0,则f(x)是周期为3的函数,则f(2010)=f(3×670)=f(0)=0;而f(2011)=f(3×670+1)=f(1)=-f(-1),代入已知的解析式,问题获解.
| 3 |
| 2 |
解答:
解:函数f(x)的定义为R,
又f(x)+f(-x)=0,∴f(-x)=-f(x),
∴f(0)=0;
因为f(x)+f(x+
)=0,所以f(x+
)=-f(x),
∴f(x+3)=-f(x+
)=f(x),∴该函数最小正周期T=3,
∴f(2010)=f(3×670)=f(0)=0,f(2011)=f(3×670+1)=f(1)=-f(-1),
又x∈(-
,0)时,f(x)=log
(1-x),
f(-1)=-1,
∴f(2011)=1.
故选:A
又f(x)+f(-x)=0,∴f(-x)=-f(x),
∴f(0)=0;
因为f(x)+f(x+
| 3 |
| 2 |
| 3 |
| 2 |
∴f(x+3)=-f(x+
| 3 |
| 2 |
∴f(2010)=f(3×670)=f(0)=0,f(2011)=f(3×670+1)=f(1)=-f(-1),
又x∈(-
| 3 |
| 2 |
| 1 |
| 2 |
f(-1)=-1,
∴f(2011)=1.
故选:A
点评:解决本题,要记住一些常见的体现函数奇偶性、周期性的结论,例如本题;同时,这道题重点考查了学生利用转化思想解题的能力,即利用奇偶性、周期性将所求化归到已知上来的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将长为8宽为4的矩形纸片卷成一个圆柱,则圆柱的最大体积为( )
| A、65π | ||
| B、32π | ||
C、
| ||
D、
|
等差数列{an}中,a1=1,公差d=5,如果an=2006,则序号n等于( )
| A、400 | B、401 |
| C、402 | D、403 |
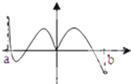 函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在(a,b)内有极小值点( )
函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在(a,b)内有极小值点( )| A、1个 | B、2个 | C、3个 | D、4个 |
用数学归纳法证明不等式
+
+…+
>
(n>2)时的过程中,由n=k到n≠k+1时,不等式的左边( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 13 |
| 24 |
A、增加了一项
| ||||||
B、增加了两项
| ||||||
C、增加了两项
| ||||||
D、增加了一项
|
已知函数f(x)=Acos(ωx+φ)的图象如图所示,f(
)=-
,则f(-
)=( )

| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|
设过抛物线的焦点F的弦为PQ,则以PQ为直径的圆与抛物线的准线的位置关系( )
| A、相交 | B、相切 |
| C、相离 | D、以上答案均有可能 |
某几何体的三视图如图所示,则它的体积是( )


A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|