题目内容
如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、
|
考点：余弦定理
专题：解三角形
分析：设出顶角为C，根据周长为底边c的5倍，用c表示出两腰长a和b，利用余弦定理表示出cosC，把三边长代入即可求出cosC的值．
解答：
解：设顶角为C，∵l=5c，
∴a=b=2c，
由余弦定理得：cosC=
=
=
．
故选：C．
∴a=b=2c，
由余弦定理得：cosC=
| b2+a2-c2 |
| 2ab |
| 4c2+4c2-c2 |
| 2×2c×2c |
| 7 |
| 8 |
故选：C．
点评：本题主要考查余弦定理的应用．余弦定理在解三角形中应用很广泛，很好的建立了三角形的边角关系，应熟练掌握．
练习册系列答案
导学全程练创优训练系列答案
相关题目
已知f（x）是R上的奇函数，且f（1）=2，f（x+3）=f（x），则f（8）=（ ）
| A、2 | B、-2 | C、0 | D、2或0 |
已知A={x|x2-4x+3≤0}，B={x|x2+mx+n＜0}，且A∩B≠∅，A∪B={x|1≤x＜4}，则m2-
n的取值范围为（ ）
| 5 |
| 2 |
| A、[15，19] |
| B、[14，18] |
| C、[15，19） |
| D、[14，18） |
等差数列{an}中，a1=1，公差d=5，如果an=2006，则序号n等于（ ）
| A、400 | B、401 |
| C、402 | D、403 |
已知函数f（x）=x3+ax2+6x-9有两个极值点x1，x2，且x12+x22=5，则a=（ ）
A、
| ||
B、-
| ||
C、±
| ||
| D、2 |
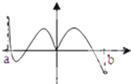函数f（x）的定义域为（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在（a，b）内有极小值点（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
已知函数f（x）=Acos（ωx+φ）的图象如图所示，f（
）=-
，则f（-
）=（ ）
| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知a是空间任意一条直线，α是一个平面，则平面α内一定存在直线与直线a（ ）
| A、相交 | B、平行 | C、异面 | D、垂直 |