题目内容
 如图,△OAB中,向量
如图,△OAB中,向量| OA |
| a |
| OB |
| b |
| OC |
| 1 |
| 2 |
| OA |
| OD |
| 2 |
| 3 |
| OB |
| OE |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点:向量在几何中的应用
专题:综合题,平面向量及应用
分析:由B,E,C三点共线,可得到一个向量等式,由A,E,D三点共线又可得到另一个等式,两者结合即可解决.
解答:
解:∵B,E,C三点共线,
∴
=x
+(1-x)
=
x
+(1-x)
,①
同理,∵A,E,D三点共线,可得
=
y
+(1-y)
,②
比较①,②,得
解得x=
,y=
,
∴
=
+
.
故选:C.
∴
| OE |
| OC |
| OB |
| 1 |
| 2 |
| a |
| b |
同理,∵A,E,D三点共线,可得
| OE |
| 2 |
| 3 |
| b |
| a |
比较①,②,得
|
解得x=
| 1 |
| 2 |
| 3 |
| 4 |
∴
| OE |
| 1 |
| 4 |
| a |
| 1 |
| 2 |
| b |
故选:C.
点评:由三点共线的条件设出参数,并利用待定系数法确定参数,利用算两次的数学思想,根据平面向量基本定理,使问题得以解决.

练习册系列答案
相关题目
已知A={x|x2-4x+3≤0},B={x|x2+mx+n<0},且A∩B≠∅,A∪B={x|1≤x<4},则m2-
n的取值范围为( )
| 5 |
| 2 |
| A、[15,19] |
| B、[14,18] |
| C、[15,19) |
| D、[14,18) |
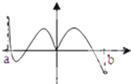 函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在(a,b)内有极小值点( )
函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在(a,b)内有极小值点( )| A、1个 | B、2个 | C、3个 | D、4个 |
已知函数f(x)=Acos(ωx+φ)的图象如图所示,f(
)=-
,则f(-
)=( )

| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|
设过抛物线的焦点F的弦为PQ,则以PQ为直径的圆与抛物线的准线的位置关系( )
| A、相交 | B、相切 |
| C、相离 | D、以上答案均有可能 |
已知函数f(x)的图象向右平移1个单位长度后关于y轴对称,当x2>x1>-1时,
>0恒成立,设a=f(-2),b=f(-
),c=f(3),则a,b,c的大小关系为( )
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 2 |
| A、c>a>b |
| B、c>b>a |
| C、a>c>b |
| D、b>a>c |
某几何体的三视图如图所示,则它的体积是( )


A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|
已知a是空间任意一条直线,α是一个平面,则平面α内一定存在直线与直线a( )
| A、相交 | B、平行 | C、异面 | D、垂直 |