题目内容
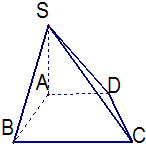 如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=
如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=| 3 |
| A、4π | B、5π | C、7π | D、8π |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:由题意,SC为外接球的直径,运用球的表面积公式求之.
解答:
解:因为SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=
,SA=2,
所以AB2+AC2=BC2,所以AB⊥AC,所以ABC所在的小圆半径为1,
过A作BC的垂线,垂足为E,构造AS,AD,2AE为长方体,则AE=
,则长方体的外接球直径为
=
=
,所以所以四棱锥的外接球的半径为r=
,
所以此四棱锥外接球表面积为4π(
)2=8π;
故选D.
| 3 |
所以AB2+AC2=BC2,所以AB⊥AC,所以ABC所在的小圆半径为1,
过A作BC的垂线,垂足为E,构造AS,AD,2AE为长方体,则AE=
| ||
| 2 |
| SA2+AD2+4AE2 |
| 4+1+3 |
| 8 |
| 2 |
所以此四棱锥外接球表面积为4π(
| 2 |
故选D.
点评:本题考查四棱锥S-ABCD的外接球表面积,考查学生的计算能力,确定四棱锥S-ABCD的外接球的半径是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±2x | ||||
D、y=±
|
设△ABC中,角A,B,C所对的边分别为a,b,c,则“∠C>90°”的一个充分非必要条件是( )
| A、sin2A+sin2B<sin2C | ||||||
B、sinA=
| ||||||
| C、c2>2(a+b-1) | ||||||
| D、sinA<cosB |
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.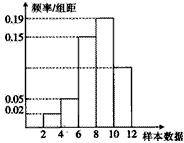 有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在[10,12)内的频数为
有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在[10,12)内的频数为