题目内容
已知f(x)是奇函数,且有f(x+1)=-
,当x∈[0,
]时,f(x)=3x,当2k+
<x<2k+1(k∈Z)时,求f(x)的解析式.
| 1 |
| f(x) |
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由f(x+1)=-
可得2是f(x)的周期,所以2k+
<x<2k+1时的解析式和
<x<1时f(x)的解析式相同,所以来求
<x<1时f(x)解析式即可.设
<x<1,f(x)=-
=
=
=3x-1,所以2k+
<x<2k+1(k∈Z)时,f(x)=3x-1.
| 1 |
| f(x) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| f(x-1) |
| 1 |
| f(1-x) |
| 1 |
| 31-x |
| 1 |
| 2 |
解答:
解:由f(x+1)=-
得:f(x+2)=-
=f(x);
∴2是函数f(x)的周期;
设-
<x<0,f(x)=-
=
,0<1-x<
,∴f(x)=
=3x-1;
当2k+
<x<2k+1(k∈Z)时,
<x-2k<1,f(x)=f(x-2k)=3x-2k-1.
| 1 |
| f(x) |
| 1 |
| f(x+1) |
∴2是函数f(x)的周期;
设-
| 1 |
| 2 |
| 1 |
| f(x-1) |
| 1 |
| f(1-x) |
| 1 |
| 2 |
| 1 |
| 31-x |
当2k+
| 1 |
| 2 |
| 1 |
| 2 |
点评:考查周期函数的概念,奇函数的概念,以及求函数解析式.

练习册系列答案
相关题目
若集合A={0,1,2,3,4},B={1,2,4}则A∪B=( )
| A、{0,1,2,3,4} |
| B、{1,2,3,4} |
| C、{1,2} |
| D、{0} |
设集合A={x∈Q|x>-1},则( )
| A、∅∉A | ||
B、
| ||
C、{
| ||
D、{
|
M是椭圆
+
=1上的点,F1、F2是椭圆的两个焦点,∠F1MF2=60°,则△F1MF2的面积等于( )
| x2 |
| 25 |
| y2 |
| 9 |
A、3
| ||
B、6
| ||
| C、3 | ||
D、2
|
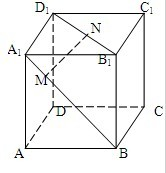 如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.
如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.