题目内容
如图,在长方体ABCD-A1B1 C1D1中,AB=AD=3cm,四棱锥A-BB1D1D的体积为6cm3,则AA1= . 

考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知得BD=3
,设四棱锥A-BB1D1D的高为h,则
×BDh=
AB×AD,再由四棱锥A-BB1D1D的体积为6,能求出AA1.
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵在长方体ABCD-A1B1 C1D1中,AB=AD=3cm,
∴BD=
=3
,
设四棱锥A-BB1D1D的高为h,
则
×BDh=
AB×AD,
解得h=
=
=
,
∵四棱锥A-BB1D1D的体积为6,
∴
×
×3
×AA1=6,
解得AA1=2(cm),
故答案为:2cm.
∴BD=
| 9+9 |
| 2 |
设四棱锥A-BB1D1D的高为h,
则
| 1 |
| 2 |
| 1 |
| 2 |
解得h=
| AB•AD |
| BD |
| 3×3 | ||
3
|
3
| ||
| 2 |
∵四棱锥A-BB1D1D的体积为6,
∴
| 1 |
| 3 |
3
| ||
| 2 |
| 2 |
解得AA1=2(cm),
故答案为:2cm.
点评:本题考查长方体的高的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
M是椭圆
+
=1上的点,F1、F2是椭圆的两个焦点,∠F1MF2=60°,则△F1MF2的面积等于( )
| x2 |
| 25 |
| y2 |
| 9 |
A、3
| ||
B、6
| ||
| C、3 | ||
D、2
|
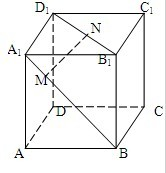 如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.
如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.