题目内容
给出下列结论:
①函数y=-tanx在区间(-
,
)上是减函数;
②不等式|2x-1|>3的解集是{x|x>2};
③m=
是两直线2x+my+1=0与mx+y-1=0平行的充分不必要条件;
④函数y=x|x-2|的图象与直线y=
有三个交点.
其中正确结论的序号是 (把所有正确结论的序号都填上)
①函数y=-tanx在区间(-
| π |
| 2 |
| π |
| 2 |
②不等式|2x-1|>3的解集是{x|x>2};
③m=
| 2 |
④函数y=x|x-2|的图象与直线y=
| 1 |
| 2 |
其中正确结论的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①,利用函数y=tanx在区间(-
,
)上是增函数可判断①;
②,利用绝对值不等式的解法可得不等式|2x-1|>3的解集是,可判断②;
③,利用充分必要条件的概念及应用可判断③;
④,作出函数y=x|x-2|的图象与直线y=
的图象,可判断④.
| π |
| 2 |
| π |
| 2 |
②,利用绝对值不等式的解法可得不等式|2x-1|>3的解集是,可判断②;
③,利用充分必要条件的概念及应用可判断③;
④,作出函数y=x|x-2|的图象与直线y=
| 1 |
| 2 |
解答:
解:对于①:∵函数y=tanx在区间(-
,
)上是增函数;
∴函数y=-tanx在区间(-
,
)上是减函数,故①正确;
对于②:∵|2x-1|>3,∴2x-1>3或2x-1<-3,解得:x>2或x<-1,
∴不等式|2x-1|>3的解集是{x|x>2或x<-1},故②错误;
对于③:∵线2x+my+1=0与直线mx+y-1=0平行,
∴2-m2=0,解得m=±
,
即m=
⇒两直线2x+my+1=0与mx+y-1=0平行,充分性成立;反之,不可,即必要性不成立,
∴m=
是两直线2x+my+1=0与mx+y-1=0平行的充分不必要条件,即③正确;
对于④:作出函数y=x|x-2|的图象与直线y=
的图象,如下:
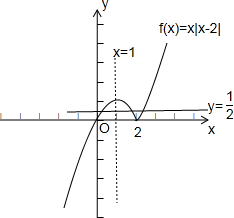
由图可知,函数y=x|x-2|的图象与直线y=
有三个交点,故④正确
故答案为:①③④.
| π |
| 2 |
| π |
| 2 |
∴函数y=-tanx在区间(-
| π |
| 2 |
| π |
| 2 |
对于②:∵|2x-1|>3,∴2x-1>3或2x-1<-3,解得:x>2或x<-1,
∴不等式|2x-1|>3的解集是{x|x>2或x<-1},故②错误;
对于③:∵线2x+my+1=0与直线mx+y-1=0平行,
∴2-m2=0,解得m=±
| 2 |
即m=
| 2 |
∴m=
| 2 |
对于④:作出函数y=x|x-2|的图象与直线y=
| 1 |
| 2 |
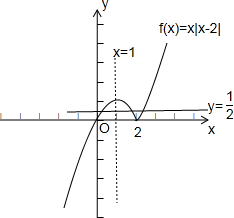
由图可知,函数y=x|x-2|的图象与直线y=
| 1 |
| 2 |
故答案为:①③④.
点评:本题考查命题的真假判断与应用,综合考查正切函数的单调性质、绝对值不等式的解法、充分必要条件的概念及应用,考查数形结合思想与转化思想.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
某几何体的三视图,如图所示,则这个几何体是( )


| A、三棱锥 | B、三棱柱 |
| C、四棱锥 | D、四棱柱 |