题目内容
圆 C1:(x+2)2+(y-2)2=4和圆C2:(x-2)2+(y-5)2=16的位置关系是( )
| A、外离 | B、相交 | C、内切 | D、外切 |
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:由条件求得两圆的圆心距 C1 C2 =5,大于半径之差而小于半径之和,从而得到两个圆相交.
解答:
解:两个圆的圆心分别为 C1(-2,2)、C2:(2,5),半径分别为2、4,
两圆的圆心距 C1 C2 =
=5,大于半径之差而小于半径之和,
故两个圆相交,
故选:B.
两圆的圆心距 C1 C2 =
| (2+2)2+(5-2)2 |
故两个圆相交,
故选:B.
点评:本题主要考查圆和圆的位置关系的判定方法,属于基础题.

练习册系列答案
相关题目
已知F是抛物线x2=4y的焦点,P是该抛物线上的动点,则线段PF中点轨迹方程是( )
A、x2=y-
| ||
B、x2=2y-
| ||
| C、x2=2y-2 | ||
| D、x2=2y-1 |
已知a∈R,则“a2<2a”是“a<2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设等差数列{an}的前n项为Sn,已知a1=-11,a3+a7=-6,当Sn取最小值时,n=( )
| A、5 | B、6 | C、7 | D、8 |
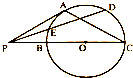 如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=
如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=