题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足a=4,b=acosC+
csinA.
(Ⅰ)求角A的大小;
(Ⅱ)当△ABC的周长最大时,求△ABC的面积.
| ||
| 3 |
(Ⅰ)求角A的大小;
(Ⅱ)当△ABC的周长最大时,求△ABC的面积.
考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:(Ⅰ)利用正弦定理把已知等式中的边转化成角的正弦,利用两角和公式化简整理后可求得tanA的值,进而求得A.
(Ⅱ)利用余弦定理构建b,c的关系式,利用基本不等式的性质求得△ABC的周长最大时,b,c的值,进而求得此时三角形的面积.
(Ⅱ)利用余弦定理构建b,c的关系式,利用基本不等式的性质求得△ABC的周长最大时,b,c的值,进而求得此时三角形的面积.
解答:
解:(Ⅰ)在△ABC中,∵b=acosC+
csinA.
∴由正弦定理得:sinB=sinAcosC+
sinCsinA,
即sin(A+C)=sinAcosC+
sinCsinA,
∴sinAcosC+cosAsinC=sinAcosC+
sinCsinA,sinC>0,
∴cosA=
sinA,即tanA=
,
∴∠A=
.
(Ⅱ)∵a=4,由余弦定理知a2=b2+c2-2bccosA,得16=b2+c2-bc,
∴16=(b+c)2-3bc,
∵bc≤
,当且仅当b=c时等号成立,
∴16≥
(b+c)2,即b+c≤8,
∴当b=c时,b+c最大,即△ABC的周长最大,
∵∠A=
,
∴△ABC的周长最大时a=b=c=4,
∴S△ABC=
bcsinA=4
.
| ||
| 3 |
∴由正弦定理得:sinB=sinAcosC+
| ||
| 3 |
即sin(A+C)=sinAcosC+
| ||
| 3 |
∴sinAcosC+cosAsinC=sinAcosC+
| ||
| 3 |
∴cosA=
| ||
| 3 |
| 3 |
∴∠A=
| π |
| 3 |
(Ⅱ)∵a=4,由余弦定理知a2=b2+c2-2bccosA,得16=b2+c2-bc,
∴16=(b+c)2-3bc,
∵bc≤
| (b+c)2 |
| 4 |
∴16≥
| 1 |
| 4 |
∴当b=c时,b+c最大,即△ABC的周长最大,
∵∠A=
| π |
| 3 |
∴△ABC的周长最大时a=b=c=4,
∴S△ABC=
| 1 |
| 2 |
| 3 |
点评:本题主要考查正弦定理和余弦定理的运用.解题的关键是利用正弦和余弦定理完成对边和角问题的转化和化归.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知圆的方程为(x-1)2+y2=1,直线l的方程为3x+4y+m=0,若圆与直线相切,则实数m的值为( )
| A、2 | B、-8 | C、2或-8 | D、0 |
 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=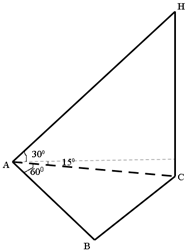 某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A、B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(结果保留根式)
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A、B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(结果保留根式)