题目内容
等差数列{an}中，已知|a5|=|a9|，公差d＞0，则使得前n项和Sn取得最小值时的正整数n为（ ）
| A、4和5 | B、5和6 |
| C、6和7 | D、7和8 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由题意可得 a5＜0、a9＞0、a5+a9=2a7=0，故前6项为负数，第7项为零，从第八项开始为正数，从而
的出结论．
的出结论．
解答：
解：由题意可得 a5＜0、a9＞0、a5+a9=2a7=0，
故前6项为负数，第7项为零，从第八项开始为正数，
故前6项或前7项的和最小，
故选：C．
故前6项为负数，第7项为零，从第八项开始为正数，
故前6项或前7项的和最小，
故选：C．
点评：本题主要考查等差数列的定义和性质，等差数列的前n项和公式，属于基础题．
练习册系列答案
相关题目
如图所示，甲 乙 丙是三个立体图形的三视图，则甲乙丙对应的标号正确的是（ ）
| A、④③② | B、②①③ |
| C、①②③ | D、③②④ |
已知数列{an}，a1=1，a2=4，且an+2=an+1-an，则数列的第6项为（ ）
| A、-1 | B、-3 | C、3 | D、-4 |
双曲线
-
=1与
-
=k始终有相同的（ ）
| x2 |
| 5 |
| y2 |
| 4 |
| x2 |
| 5 |
| y2 |
| 4 |
| A、焦点 | B、准线 |
| C、渐近线 | D、离心率 |
已知x＞0，n∈N*，由下列结论x+
≥2，x+
≥3，x+
≥4，…，得到一个正确的结论可以是（ ）
| 1 |
| x |
| 4 |
| x2 |
| 27 |
| x3 |
A、x+
| ||
B、x+
| ||
C、x+
| ||
D、x+
|
定义A㊣B、B㊣C、C㊣D、D㊣A的运算分别对应图中的（1）、（2）、（3）、（4）．则图中的甲、乙的运算式可以表示为：（ ）
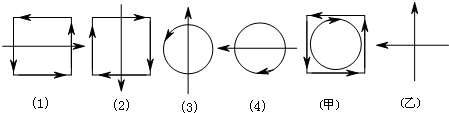
| A、B㊣D、C㊣A |
| B、B㊣D、A㊣C |
| C、D㊣B、C㊣A |
| D、D㊣B、A㊣C |
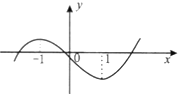已知函数f（x）=ax3+bx2+cx+d图象如图所示，f′（x）是f（x）的导函数，则不等式| f′(x) |
| x |
| A、（-∞，-1）∪（0，1） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-1，0）∪（0，1） |
| D、（-1，0）∪（1，+∞） |