题目内容
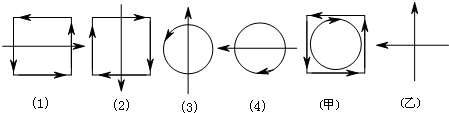
定义A㊣B、B㊣C、C㊣D、D㊣A的运算分别对应图中的（1）、（2）、（3）、（4）．则图中的甲、乙的运算式可以表示为：（ ）
| A、B㊣D、C㊣A |
| B、B㊣D、A㊣C |
| C、D㊣B、C㊣A |
| D、D㊣B、A㊣C |
考点：进行简单的合情推理
专题：推理和证明
分析：根据已知图象与运算的关系，进行必要的分析归纳，找出规律，猜想未知的图象与运算的关系．
解答：
解：通过观察可知：A在前表示向右的“-”在后表示向左的“-”，
B在前表示顺时针的“□”，再后表示逆时针的“□”，
C在前表示向上的“|”，在后表示向下的“|”，
D在前表示顺时针的“○”，在后表示逆时针的“○”．
图中的（甲）、（乙）所对应的运算结果可能是D㊣B、C㊣A，
故选C．
B在前表示顺时针的“□”，再后表示逆时针的“□”，
C在前表示向上的“|”，在后表示向下的“|”，
D在前表示顺时针的“○”，在后表示逆时针的“○”．
图中的（甲）、（乙）所对应的运算结果可能是D㊣B、C㊣A，
故选C．
点评：本题考查的是归纳推理的应用，方法是根据已知图象与运算的关系，进行必要的分析归纳，找出规律，猜想未知的图象与运算的关系，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=xsinx，x∈[-
，
]，则f（
），f（1），f（-
）的大小关系为（ ）
| π |
| 2 |
| π |
| 2 |
| π |
| 5 |
| π |
| 3 |
A、f（-
| ||||
B、f（1）＞f（-
| ||||
C、f（
| ||||
D、f（-
|
等差数列{an}中，已知|a5|=|a9|，公差d＞0，则使得前n项和Sn取得最小值时的正整数n为（ ）
| A、4和5 | B、5和6 |
| C、6和7 | D、7和8 |
已知a＞3，则z=
+a的最小值是（ ）
| 1 |
| a-3 |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
如图所示将若干个点摆成三角形图案，每条边（色括两个端点）有n（n＞l，n∈N*）个点，相应的图案中总的点数记为an，则
+
+
+…+
=（ ）
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2013a2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的左、右焦点分别为F1，F2，渐进线为l1，l2，以F1F2为直径的圆在第一象限与l1交于点P，在第二象限与l2交于点Q，且
+
=λ
（λ＞0），则双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OF1 |
| OP |
| OQ |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
在数列{an}中，已知a3=1，a5=3，a7=9，则{an}一定（ ）
| A、是等差数列 |
| B、是等比数列 |
| C、不是等差数列 |
| D、不是等比数列 |