题目内容
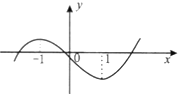 已知函数f(x)=ax3+bx2+cx+d图象如图所示,f′(x)是f(x)的导函数,则不等式
已知函数f(x)=ax3+bx2+cx+d图象如图所示,f′(x)是f(x)的导函数,则不等式| f′(x) |
| x |
| A、(-∞,-1)∪(0,1) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-1,0)∪(0,1) |
| D、(-1,0)∪(1,+∞) |
考点:利用导数研究函数的单调性
专题:导数的综合应用,不等式的解法及应用
分析:先从原函数的极值点处得出导数的零点,再利用导函数是二次函数的特点,结合二次函数的图象,即可解出不等式x•f′(x)<0的解集.
解答:
 解:由图可知:
解:由图可知:
±1是函数f(x)=ax3+bx2+cx+d的两个极值点;
即±1是导函数f′(x)=3ax2+2bx+c的两个零点;
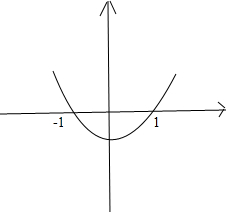
根据图象知:x∈(-∞,-1)时,f′(x)>0,所以函数f′(x)的图象应开口向上,所以导函数图象如下图:
由图可得,
>0的解集是:(-1,0)∪(1,+∞),
故答案是D.
 解:由图可知:
解:由图可知:±1是函数f(x)=ax3+bx2+cx+d的两个极值点;
即±1是导函数f′(x)=3ax2+2bx+c的两个零点;
根据图象知:x∈(-∞,-1)时,f′(x)>0,所以函数f′(x)的图象应开口向上,所以导函数图象如下图:
由图可得,
| f′(x) |
| x |
故答案是D.
点评:通过观察原图,要看出来±1是原函数的两个极值点,从而是导函数的两个零点,知道这点就可画出导函数的图象,根据导函数的图象便较容易求出原不等式的解.考察极值的概念,观察图象的能力,对二次函数图象的掌握,不等式的解法.

练习册系列答案
相关题目
已知函数f(x)=
x3-
(2a+1)x2+(a2+a)x,若对任意m∈R,直线y=kx+m都不是曲线y=f(x)的切线,则实数k的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||
B、(-
| ||
C、(-∞,-
| ||
D、(-∞,-
|
等差数列{an}中,已知|a5|=|a9|,公差d>0,则使得前n项和Sn取得最小值时的正整数n为( )
| A、4和5 | B、5和6 |
| C、6和7 | D、7和8 |
如图所示将若干个点摆成三角形图案,每条边(色括两个端点)有n(n>l,n∈N*)个点,相应的图案中总的点数记为an,则
+
+
+…+
=( )

| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2013a2014 |

A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,渐进线为l1,l2,以F1F2为直径的圆在第一象限与l1交于点P,在第二象限与l2交于点Q,且
+
=λ
(λ>0),则双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| OF1 |
| OP |
| OQ |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
抛物线y2=4x,M(1,1)为其弦AB的中点,则AB方程为( )
| A、4x-2y-1=0 |
| B、4x-2y+1=0 |
| C、2x-y-1=0 |
| D、2x-y+1=0 |
在数列{an}中,已知a3=1,a5=3,a7=9,则{an}一定( )
| A、是等差数列 |
| B、是等比数列 |
| C、不是等差数列 |
| D、不是等比数列 |
对于方程|x2-3x+2|=m(x-
)的实根个数,以下说法正确的是( )
| 3 |
| 2 |
| A、存在实数m,使得方程无解 |
| B、存在实数m,使得方程恰有1根 |
| C、无论m取任何实数,方程恰有2根 |
| D、无论m取任何实数,方程恰有4根 |