题目内容
已知x＞0，n∈N*，由下列结论x+
≥2，x+
≥3，x+
≥4，…，得到一个正确的结论可以是（ ）
| 1 |
| x |
| 4 |
| x2 |
| 27 |
| x3 |
A、x+
| ||
B、x+
| ||
C、x+
| ||
D、x+
|
考点：归纳推理
专题：推理和证明
分析：通过观察可以发现，每一个不等式的右边的数都是对应的个数加1，左边的分式中分子是对应个数的数字的相应次方，
解答：
解：x+
≥2，x+
≥3，x+
≥4，…，
每一个不等式的右边的数都是对应的个数加1，左边的分式中分子是对应个数的数字的相应次方，
于是可以得到结论为x+
≥n+1．
故选：D．
| 1 |
| x |
| 4 |
| x2 |
| 27 |
| x3 |
每一个不等式的右边的数都是对应的个数加1，左边的分式中分子是对应个数的数字的相应次方，
于是可以得到结论为x+
| nn |
| xn |
故选：D．
点评：本题主要考查了归纳推理的问题，找到规律是关键，属于基础题．
练习册系列答案
相关题目
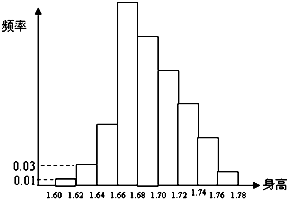为了解某校身高在1.60m～1.78m的高一学生的情况，随机地抽查了该校100名高一学生，得到如图所示频率直方图．由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为m，身高在1.66m～1.74m的学生数为n，则m，n的值分别为（ ）| A、0.27，78 |
| B、0.27，83 |
| C、0.81，78 |
| D、0.09，83 |
一个盒子内装有4张卡片，每张卡片上依次写有如下4个定义在R上的函数中的一个f（x）=sinx，g（x）=cosx，h（x）=x3，k（x）=x4，现从盒子中任取两张卡片，将卡片上的函数相乘得到一个新函数，则所得新函数是偶函数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
等差数列{an}中，已知|a5|=|a9|，公差d＞0，则使得前n项和Sn取得最小值时的正整数n为（ ）
| A、4和5 | B、5和6 |
| C、6和7 | D、7和8 |
已知△ABC中，a=b=4，c=4
，则∠C=（ ）
| 3 |
| A、150° |
| B、30°或150° |
| C、120° |
| D、60°或120° |
如图所示将若干个点摆成三角形图案，每条边（色括两个端点）有n（n＞l，n∈N*）个点，相应的图案中总的点数记为an，则
+
+
+…+
=（ ）
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2013a2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
抛物线y2=4x，M（1，1）为其弦AB的中点，则AB方程为（ ）
| A、4x-2y-1=0 |
| B、4x-2y+1=0 |
| C、2x-y-1=0 |
| D、2x-y+1=0 |
已知函数f（x）=cosx-
（x∈R，x≠0），则f′（1）值为（ ）
| 1 |
| x |
| A、-1-sin1 |
| B、1+sin1 |
| C、-1+sin1 |
| D、1-sin1 |