题目内容
如图所示，甲 乙 丙是三个立体图形的三视图，则甲乙丙对应的标号正确的是（ ）
| A、④③② | B、②①③ |
| C、①②③ | D、③②④ |
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：根据甲、乙、丙的三视图，得出甲、乙、丙各是什么几何体．
解答：
解：根据甲、乙、丙的三视图，得出甲是圆柱体，乙是三棱锥，丙是圆锥；
∴甲乙丙对应的标号应是④③②．
故选：A．
∴甲乙丙对应的标号应是④③②．
故选：A．
点评：本题考查了空间几何体的三视图的知识，解题时应根据几何体的三视图能判断该几何体是什么，是基础题．
练习册系列答案
字词句段篇系列答案
相关题目
已知函数f（x）=
x3-
（2a+1）x2+（a2+a）x，若对任意m∈R，直线y=kx+m都不是曲线y=f（x）的切线，则实数k的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||
B、（-
| ||
C、（-∞，-
| ||
D、（-∞，-
|
实验女排和育才女排两队进行比赛，在一局比赛中实验女排获胜的概率是
，没有平局．若采用三局两胜制，即先胜两局者获胜且比赛结束，则实验女排获胜的概率等于（ ）
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
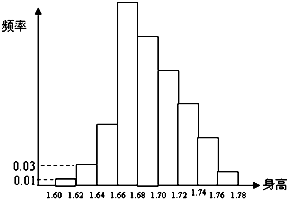为了解某校身高在1.60m～1.78m的高一学生的情况，随机地抽查了该校100名高一学生，得到如图所示频率直方图．由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为m，身高在1.66m～1.74m的学生数为n，则m，n的值分别为（ ）| A、0.27，78 |
| B、0.27，83 |
| C、0.81，78 |
| D、0.09，83 |
已知函数f（x）=xsinx，x∈[-
，
]，则f（
），f（1），f（-
）的大小关系为（ ）
| π |
| 2 |
| π |
| 2 |
| π |
| 5 |
| π |
| 3 |
A、f（-
| ||||
B、f（1）＞f（-
| ||||
C、f（
| ||||
D、f（-
|
等差数列{an}中，已知|a5|=|a9|，公差d＞0，则使得前n项和Sn取得最小值时的正整数n为（ ）
| A、4和5 | B、5和6 |
| C、6和7 | D、7和8 |
在数列{an}中，已知a3=1，a5=3，a7=9，则{an}一定（ ）
| A、是等差数列 |
| B、是等比数列 |
| C、不是等差数列 |
| D、不是等比数列 |