题目内容
若数列{an},{bn}的通项公式分别是an=(-1)n+2012•a,bn=2+
,且an<bn对任意n∈N*恒成立,则实数a的取值范围是 .
| (-1)n+2013 |
| n |
考点:数列与不等式的综合
专题:计算题,点列、递归数列与数学归纳法
分析:讨论n取奇数和偶数时,利用不等式恒成立,即可确定a的取值范围.
解答:
解:∵an=(-1)n+2012•a,bn=2+
,且an<bn对任意n∈N*恒成立,
∴(-1)n+2012•a<2+
,
若n为偶数,则不等式等价为a<2-
,即a<2-
,即a<
;
若n为奇数,则不等式等价为-a<2+
,即有-a≤2,即a≥-2.
综上,-2≤a<
.
即实数a的取值范围是[-2,
).
故答案为:[-2,
).
| (-1)n+2013 |
| n |
∴(-1)n+2012•a<2+
| (-1)n+2013 |
| n |
若n为偶数,则不等式等价为a<2-
| 1 |
| n |
| 1 |
| 2 |
| 3 |
| 2 |
若n为奇数,则不等式等价为-a<2+
| 1 |
| n |
综上,-2≤a<
| 3 |
| 2 |
即实数a的取值范围是[-2,
| 3 |
| 2 |
故答案为:[-2,
| 3 |
| 2 |
点评:本题主要考查不等式恒成立问题,讨论n取奇数和偶数是解决本题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
下列说法正确的是( )
| A、a?α,b?β,则a与b是异面直线 |
| B、a与b异面,b与c异面,则a与c异面 |
| C、a,b不同在平面α内,则a与b异面 |
| D、a,b不同在任何一个平面内,则a与b异面 |
已知关于x的一元二次方程x2-(k-1)x+1=0有两个实根,则k的取值范围为( )
| A、[-1,3] |
| B、(-∞,-1]∪[3,+∞) |
| C、(-1,3) |
| D、(-∞,-1)∪(3,+∞) |
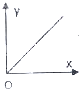
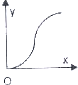
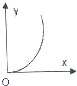
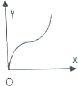
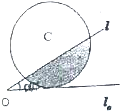 如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )
如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )