题目内容
11.已知△ABC的顶点A(5,1),AB边上的中线CM所在的直线方程为2x-y-5=0,AC边上的高BH所在直线的方程为x-2y-5=0.(1)求直线BC的方程;
(2)求直线BC关于CM的对称直线方程.
分析 (1)由已知得直线AC的方程为:2x+y-11=0.联立$\left\{\begin{array}{l}{2x+y-11=0}\\{2x-y-5=0}\end{array}\right.$,解得C坐标.设B(a,b),则M$(\frac{a+5}{2},\frac{b+1}{2})$.M在直线2x-y-5=0上,可得:$2×\frac{a+5}{2}$-$\frac{b+1}{2}$-5=0,化为:2a-b-1=0.B在直线x-2y-5=0上,可得:a-2b-5=0.联立联立解得B坐标.可得直线BC的方程.
(2)点B关于直线CM对称的点B(x,y)在所求的直线上,由$\left\{\begin{array}{l}{2×\frac{x-1}{2}-\frac{y-3}{2}-5=0}\\{\frac{y+3}{x+1}×2=-1}\end{array}\right.$,解得B即可得出所求直线方程.
解答 解:(1)由已知得直线AC的方程为:2x+y-11=0.
联立$\left\{\begin{array}{l}{2x+y-11=0}\\{2x-y-5=0}\end{array}\right.$,解得C(4,3).
设B(a,b),则M$(\frac{a+5}{2},\frac{b+1}{2})$.
M在直线2x-y-5=0上,可得:$2×\frac{a+5}{2}$-$\frac{b+1}{2}$-5=0,化为:2a-b-1=0.
B在直线x-2y-5=0上,可得:a-2b-5=0.
联立$\left\{\begin{array}{l}{2a-b-1=0}\\{a-2b-5=0}\end{array}\right.$,解得a=-1,b=-3,B(-1,-3).
于是直线BC的方程为:6x-5y-9=0.
(2)点B关于直线CM对称的点B(x,y)在所求的直线上,
由$\left\{\begin{array}{l}{2×\frac{x-1}{2}-\frac{y-3}{2}-5=0}\\{\frac{y+3}{x+1}×2=-1}\end{array}\right.$,B$(\frac{11}{5},-\frac{23}{5})$.
∴直线BC关于CM的对称直线方程为38x-9y-125=0.
点评 本题考查了直线垂直与斜率之间的关系、直线相交与方程组的关系,考查了推理能力与计算能力,属于中档题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | 6 |
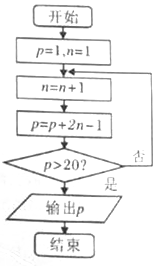
| A. | 49 | B. | 36 | C. | 25 | D. | 16 |
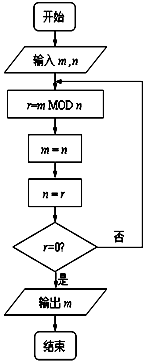 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMOD n”表示m除以n的余数),若输入的m,n分别为72,15,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMOD n”表示m除以n的余数),若输入的m,n分别为72,15,则输出的m=( )| A. | 12 | B. | 3 | C. | 15 | D. | 45 |
| A. | {x|-3<x<1} | B. | {x|-1<x<3}. | C. | {x|x<-3或x>1} | D. | {x|x<-1或x>3} |
 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )