题目内容
20.函数f(x)=ln(-x2+2x+3)的定义域为( )| A. | {x|-3<x<1} | B. | {x|-1<x<3}. | C. | {x|x<-3或x>1} | D. | {x|x<-1或x>3} |
分析 根据对数函数的真数大于0,列出不等式-x2+2x+3>0求解集即可.
解答 解:函数f(x)=ln(-x2+2x+3),
∴-x2+2x+3>0,
即x2-2x-3<0,
解得-1<x<3,
∴函数f(x)的定义域为{x|-1<x<3}.
故选:B.
点评 本题考查了一元二次不等式的解法与应用问题,是基础题.

练习册系列答案
相关题目
8.一个三棱锥的三视图如下图所示,则该几何体的体积为( )
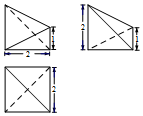

| A. | 1 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{8\sqrt{3}}{3}$ |
15.程序框图如图所示,若输入a的值是虚数单位i,则输出的结果是( )


| A. | -1 | B. | i-1 | C. | 0 | D. | -i |
9.设z=-1+3i,则z的共轭复数为( )
| A. | -1+3i | B. | -1-3i | C. | 1+3i | D. | 1-3i |
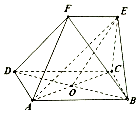 如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF
如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF