已知a.b∈R.i是虚数单位.若a-i与2+bi互为共轭复数.且z=2.则z在复平面中所表示的点在第( )象限．A．一B．二C．三D．四题目和参考答案——青夏教育精英家教网—

题目内容

1．已知a，b∈R，i是虚数单位，若a-i与2+bi互为共轭复数，且z=（a+bi）²，则z在复平面中所表示的点在第（　　）象限．

A．

一

B．

二

C．

三

D．

四

分析利用共轭复数的概念求得a，b的值，代入z=（a+bi）²，展开后求出z的坐标得答案．

解答解：∵a-i与2+bi互为共轭复数，
∴a=2，b=1，
则z=（a+bi）²=（2+i）²=3+4i，
∴z在复平面中所表示的点的坐标为（3，4），在第一象限．
故选：A．

点评本题考查复数代数形式的乘法运算，考查复数的代数表示法及其几何意义，是基础题．

练习册系列答案

12．已知$sinx=\frac{{\sqrt{5}}}{5}，（{0＜x＜\frac{π}{2}}）$，
（1）求cosx，tanx；
（2）求$\frac{cosx+2sinx}{2cosx-sinx}$．

9．设z=-1+3i，则z的共轭复数为（　　）

16．一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的外接球的体积为（　　）

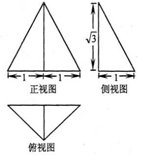
A．

$\frac{\sqrt{3}}{3}$π

$\frac{32\sqrt{3}}{27}$π

6．下列是我国2010年至2016年生活垃圾无害化处理量（单位：亿吨）的折线图．

（1）由折线图看出，可用线性回归模型拟合y与t的关系，求y关于t的回归方程（系数精确到0.01）；
（2）预测2018年我国生活垃圾无害化处理量．
附注：参考数据：$\sum_{i=1}^{7}$y_i=9.32，$\sum_{i=1}^{7}$t_iy_i=40.17
回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$t中斜率和截距的最小二乘法估计公式分别为：
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$．

13．已知$\frac{π}{4}＜α＜\frac{3π}{4}，0＜β＜\frac{π}{4}，cos（\frac{π}{4}+α）=-\frac{4}{5}，sin（\frac{3π}{4}+β）=\frac{12}{13}$．
（1）求sin（α+β）的值；
（2）求cos（α-β）的值．

10．是否存在a，b，c使等式（$\frac{1}{n}$）²+（$\frac{2}{n}$）²+（$\frac{3}{n}$）²+…+（$\frac{n}{n}$）²=$\frac{a{n}^{2}+bn+c}{n}$对一切n∈N^*都成立若不存在，说明理由；若存在，用数学归纳法证明你的结论．

11．把函数y=sinx（x∈R）的图象上所有点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再把所得图象上所有向左平行移动$\frac{π}{3}$个单位长度，得到的图象所表示的函数是（　　）

A．

$y=sin（2x-\frac{π}{3}），x∈R$

B．

$y=sin（\frac{x}{2}+\frac{π}{6}），x∈R$

C．

$y=sin（2x+\frac{π}{3}），x∈R$

D．

$y=sin（2x+\frac{2π}{3}），x∈R$

试题分类