题目内容
6.已知f(x)满足f′(2)=3,则$\underset{lim}{{x}_{0}→0}$$\frac{f(2+{2x}_{0})-f(2)}{{x}_{0}}$=( )| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | 6 |
分析 利用导数的定义,即可求解.
解答 解:∵f′(2)=3,
∴$\underset{lim}{{x}_{0}→0}$$\frac{f(2+{2x}_{0})-f(2)}{{x}_{0}}$=2$\underset{lim}{{x}_{0}→0}$$\frac{f(2+2{x}_{0})-f(2)}{2{x}_{0}}$=2f′(2)=6,
故选D.
点评 本题考查导数的定义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
16.已知圆x2+y2+2x-6y+5=0,将直线y=2x+λ向上平移2个单位与之相切,则实数λ的值为( )
| A. | -7或3 | B. | -2或8 | C. | -4或4 | D. | 0或6 |
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,O为坐标原点,点M,N是双曲线C上异于顶点的关于原点对称的两点,P是双曲线C上任意一点,PM,PN的斜率都存在,则kPM•kPN的值为( )
| A. | $\frac{a^2}{b^2}$ | B. | $\frac{b^2}{a^2}$ | C. | $\frac{b^2}{c^2}$ | D. | 以上答案都不对 |
15.程序框图如图所示,若输入a的值是虚数单位i,则输出的结果是( )


| A. | -1 | B. | i-1 | C. | 0 | D. | -i |
16.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的体积为( )
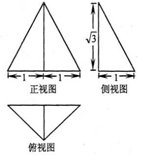

| A. | $\frac{\sqrt{3}}{3}$π | B. | π | C. | $\frac{26}{3}$π | D. | $\frac{32\sqrt{3}}{27}$π |
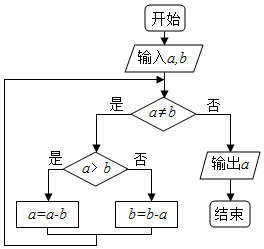 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为24,18,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为24,18,则输出的a=( )