题目内容
5.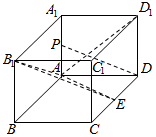 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.(1)求证:B1E⊥AD1;
(2)若E为CD的中点,P是AA1的中点,求证DP∥平面B1AE.
分析 (1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能证明B1E⊥AD1.
(2)求出$\overrightarrow{DP}$和平面B1AE的法向量,利用向量法能证明DP∥平面B1AE.
解答 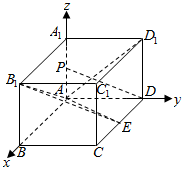 证明:(1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
证明:(1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
∵AA1=AD=a,E为CD上任意一点,设DE=t,DC=2m,0≤t≤2m,
∴B1(2m,0,a),E(m,a,0),A(0,0,0),D1(0,a,a),
$\overrightarrow{{B}_{1}E}$=(-m,a,-a),$\overrightarrow{A{D}_{1}}$=(0,a,a),
$\overrightarrow{{B}_{1}E}$•$\overrightarrow{A{D}_{1}}$=0+a2-a2=0,
∴B1E⊥AD1.
(2)P(0,0,$\frac{a}{2}$),D(0,a,0),B1(2m,0,a),A(0,0,0),E(m,a,0),
$\overrightarrow{DP}$=(0,-a,$\frac{a}{2}$),$\overrightarrow{A{B}_{1}}$=(2m,0,a),$\overrightarrow{AE}$=(m,a,0),
设平面B1AE的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{A{B}_{1}}=2mx+az=0}\\{\overrightarrow{m}•\overrightarrow{AE}=mx+ay=0}\end{array}\right.$,
取z=2,得$\overrightarrow{m}$=(-$\frac{a}{m}$,1,2),
∵$\overrightarrow{DP}•\overrightarrow{m}$=0-a+a=0,且DP?平面B1AE,
∴DP∥平面B1AE.
点评 本题考查异面直线垂直的证明,考查线面平行的证明,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | ?x∈(0,+∞),3x<x3 | B. | ?x∈(0,+∞),3x>x3 | C. | ?x∈(0,+∞),3x≥x3 | D. | ?x∈(0,+∞),3x≥x3 |
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
| A. | ?x0∈R,使得${3^{x_0}}≤0$ | |
| B. | “$x=\frac{π}{6}$”是“$cosx=\frac{{\sqrt{3}}}{2}$”的必要不充分条件 | |
| C. | ?x∈R+,lgx>0 | |
| D. | “x=1”是“x≥1”的充分不必要条件 |