题目内容
15.已知f(x)是定义在R上的奇函数,当x>0时,f(x)=1+log${\;}_{\frac{1}{2}}$x,则f(-4)=1.分析 由题意可得f(-4)=-f(4),计算求得结果.
解答 解:f(-4)=-f(4)=-(1+${log}_{\frac{1}{2}}4$ )=-1+2=1,
故答案为:1.
点评 本题主要考查函数的奇偶性的应用,求函数的值,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
20.设过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,c=$\sqrt{{a}^{2}-{b}^{2}}$)的左焦点与上顶点的直线为l,若坐标原点O到直线l的距离为$\frac{c}{2}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
7.设全集U=R,A={x∈N|-1≤x≤10},B={x∈R|x2-x-6=0},则图中阴影部分表示的集合为( )
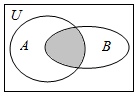

| A. | {3} | B. | {2} | C. | {3,2} | D. | {-2,3} |
4.已知全集U={l,2,3,4,5},集合A={2,3,4},B={l,4}则(∁UA)∩B为( )
| A. | {1} | B. | {1,5} | C. | {1,4} | D. | {1,4,5} |
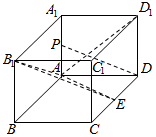 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.