题目内容
10.已知x,y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ x+y≤2\\ y≥0\end{array}\right.$,则z=3x-y的最大值是( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
分析 作出可行域,再作出直线l0:y=3x,将l0平移与可行域有公共点,直线y=3x-z在y轴上的截距最小时,z有最大值,求出此时直线y=3x-z经过的可行域内的点的坐标,代入z=3x-y中即可.
解答 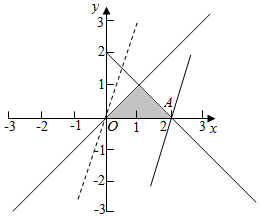 解:如图,作出约束条件$\left\{\begin{array}{l}x-y≥0\\ x+y≤2\\ y≥0\end{array}\right.$的可行域,
解:如图,作出约束条件$\left\{\begin{array}{l}x-y≥0\\ x+y≤2\\ y≥0\end{array}\right.$的可行域,
作出直线l0:y=3x,
由$\left\{\begin{array}{l}{y=0}\\{x+y=2}\end{array}\right.$得A(2,0),
将l0平移至过点A(2,0)处时,
函数z=3x-y有最大值6.
故选:D.
点评 本题考查线性规划问题,考查数形结合思想,解答的步骤是有两种方法:一种是:画出可行域画法,标明函数几何意义,得出最优解.另一种方法是:由约束条件画出可行域,求出可行域各个角点的坐标,将坐标逐一代入目标函数,验证,求出最优解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
18.已知一个总体中有100个个体,将其随机编号为0,1,2,…10.现用系统抽样法抽取一个容量为10的样本,规定如果在第1组中随机抽取的号码为m,那么在第k组抽取的号码的个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码为( )
| A. | 63 | B. | 66 | C. | 73 | D. | 76 |
15.已知双曲线与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点重合,它们的离心率之和为$\frac{14}{5}$,则双曲线的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\frac{5}{3}x$ | C. | $y=±\frac{3}{5}x$ | D. | $y=±\sqrt{3}x$ |
2.若复数z满足zi=1+2i,则复数z的共轭复数$\overline{z}$=( )
| A. | -2-i | B. | -2+i | C. | 2-i | D. | 2+i |
20.设过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,c=$\sqrt{{a}^{2}-{b}^{2}}$)的左焦点与上顶点的直线为l,若坐标原点O到直线l的距离为$\frac{c}{2}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
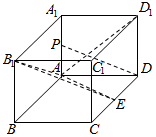 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.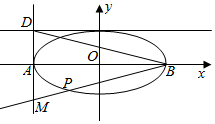 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.