题目内容
13.下列命题:①已知m,n表示两条不同的直线,α,β表示两个不同的平面,并且m⊥α,n?β,则“α⊥β”是“m∥n”的必要不充分条件;
②不存在x∈(0,1),使不等式成立log2x<log3x;
③“若am2<bm2,则a<b”的逆命题为真命题;
④?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数.
正确的命题序号是①.
分析 ①根据面面垂直的判定定理以及充分条件和必要条件的定义进行判断,
②根据对数函数的单调性的性质进行判断,
③根据四种命题之间的关系进行判断,
④根据三角函数的奇偶性进行判断.
解答 解:①∵m⊥α,若m∥n,
∴n⊥α,
∵n?β,∴α⊥β,即必要性成立,反之不一定成立,即“α⊥β”是“m∥n”的必要不充分条件; 故①正确,
②若log2x<log3x,则$\frac{1}{lo{g}_{x}2}$<$\frac{1}{lo{g}_{x}3}$,
若x>1,则logx2>logx3,此时不等式不成立,
若0<x<1,则logx2>logx3,此时不等式恒成立,
即?x∈(0,1),不等式成立log2x<log3x成立,故②错误,
③“若am2<bm2,则a<b”的逆命题为若a<b,则am2<bm2,为假命题.,当m=0时,am2<bm2不成立,故③错误;
④当θ=$\frac{π}{2}$函数f(x)=sin(2x+θ)=cos2x是偶函数.故④错误,
故答案为:①
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
8.执行如图所示的程序框图,输出S的值为$\frac{1}{2}$时,k是( )
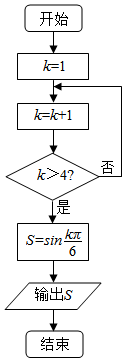

| A. | 5 | B. | 3 | C. | 4 | D. | 2 |
18.已知一个总体中有100个个体,将其随机编号为0,1,2,…10.现用系统抽样法抽取一个容量为10的样本,规定如果在第1组中随机抽取的号码为m,那么在第k组抽取的号码的个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码为( )
| A. | 63 | B. | 66 | C. | 73 | D. | 76 |
2.若复数z满足zi=1+2i,则复数z的共轭复数$\overline{z}$=( )
| A. | -2-i | B. | -2+i | C. | 2-i | D. | 2+i |
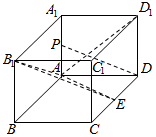 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.