��Ŀ����
1����֪��ƽ��ֱ������ϵxoy�У�ֱ��l�IJ���������$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t+4\sqrt{2}}\end{array}\right.$��t�Dz���������ԭ��O Ϊ���㣬O xΪ���Ὠ��������ϵ��ԲC �ļ����귽��Ϊ$��=2cos����+\frac{��}{4}��$����1����ֱ��l����ͨ���̺�Բ��C ��ֱ�����ꣻ
��2����ֱ��l�ϵĵ���ԲC�����ߣ������߳�����Сֵ��
���� ��1���������ַ��̵Ļ���������������ֱ��l����ͨ���̺�Բ��C ��ֱ�����ꣻ
��2��ԲC�İ뾶r=1�����Բ�ĵ�ֱ�ߵľ��룬���������߳�����Сֵ��
��� �⣺��1��ֱ��l����ͨ����Ϊ$y=x+4\sqrt{2}$��
��$��=2cos����+\frac{��}{4}��$��${��^2}=\sqrt{2}��cos��-\sqrt{2}��sin��$
��ԲC����ͨ����Ϊ${x^2}+{y^2}=\sqrt{2}x-\sqrt{2}y$����${x^2}+{y^2}-\sqrt{2}x+\sqrt{2}y=0$
Բ��C��ֱ������Ϊ $��\frac{{\sqrt{2}}}{2}��-\frac{{\sqrt{2}}}{2}��$��
��2��ԲC�İ뾶r=1��Բ�ĵ�ֱ�ߵľ���$d=\frac{{|\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}+4\sqrt{2}|}}{{\sqrt{2}}}=5$
�����߳�����СֵΪ$\sqrt{{d^2}-{r^2}}=\sqrt{{5^2}-{1^2}}=\sqrt{6��4}=2\sqrt{6}$��
���� ���⿼�����ַ��̵Ļ���������ֱ����Բ��λ�ù�ϵ������ѧ���ļ��������������е��⣮

��ϰ��ϵ�д�
 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
�����Ŀ
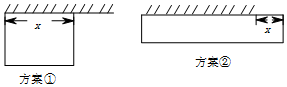 �Ϻ��и��˸���ѧ���ڸ�����������2015��9����ʽ��ʼ������ҪΧ��һ�������900ƽ���ľ��εس��ص�Χǽ����һ�泤��Ϊ20�ľ�ǽ��ͼ��б�ܲ������мס�������ά�����þ�ǽ������
�Ϻ��и��˸���ѧ���ڸ�����������2015��9����ʽ��ʼ������ҪΧ��һ�������900ƽ���ľ��εس��ص�Χǽ����һ�泤��Ϊ20�ľ�ǽ��ͼ��б�ܲ������мס�������ά�����þ�ǽ������