设函数f(x)=xex.则函数f(x)的单调递增区间为．题目和参考答案——青夏教育精英家教网——

题目内容

13．设函数f（x）=xe^x，则函数f（x）的单调递增区间为（-1，+∞）．

分析求出导函数，利用f′（x）＞0即可得出．

解答解：f′（x）=e^x+xe^x=（1+x）e^x，
令f′（x）＞0，解得x＞-1，
∴f（x）=xe^x的单调递增区间是（-1，+∞）．
故答案是（-1，+∞）．

点评本题考查了导数与函数单调性的关系，属于基础题．

练习册系列答案

假期作业寒假成长乐园中国少年儿童出版社系列答案

优加学案中考真题详解汇编系列答案

同行课课100分过关作业系列答案

举一反三全能训练系列答案

快乐的假期生活寒假作业哈尔滨出版社系列答案

寒假作业陕西人民教育出版社系列答案

活力假期期末寒假衔接系列答案

新锐图书复习计划期末寒假衔接系列答案

高考导航系列丛书假期作业寒假系列答案

寒假作业教育科学出版社系列答案

相关题目

3．若实数x，y满足xy=1，则x²+3y²的最小值为2$\sqrt{3}$．

4．点A（-2，-2），B（-2，6），C（4，-2），点P在圆x²+y²=4上运动，则|PA|²+|PB|²+|PC|²的最大值，最小值分别为（　　）

1．已知在平面直角坐标系xoy中，直线l的参数方程是$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t+4\sqrt{2}}\end{array}\right.$（t是参数），以原点O 为极点，O x为极轴建立极坐标系，圆C 的极坐标方程为$ρ=2cos（θ+\frac{π}{4}）$．
（1）求直线l的普通方程和圆心C 的直角坐标；
（2）由直线l上的点向圆C引切线，求切线长的最小值．

8．下列命题中正确命题的个数是（　　）
（1）设f（x）=ax³+bx²+cx+d（a≠0），若f（x）存在极值，则一定既有极大值又有极小值；
（2）命题“若m=3，则椭圆$\frac{x^2}{4}+\frac{y^2}{m}$=1离心率为$\frac{1}{2}$”的逆命题；
（3）设z∈C，命题“若z为实数，则z=$\overline{z}$”的否命题；
（4）设a，b∈R，命题“若ab=0，则复数z=a+bi为纯虚数”的逆否命题．

18．已知f（x）=$\frac{1}{2}{x^2}$-alnx（a＞0），x∈[1，e]．
（1）若f（x）的最小值为0，求实数a的值；
（2）若f（x）恰有两个零点，求实数a的取值范围．

5．设z=3x+4y，式中变量x，y满足下列条件：$\left\{\begin{array}{l}{x+2y≤12}\\{2x+y≤16}\\{-x+2y≤0}\\{x≥0，y≥0}\end{array}\right.$，求z的最大值和最小值．

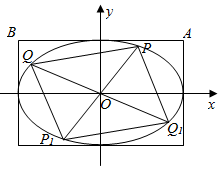已知椭圆C的中心在原点，对称轴为坐标轴，左焦点为F₁（-1，0），离心率为$\frac{1}{2}$．
（1）求椭圆C标准方程；
（2）分别以椭圆C的四个顶点作坐标轴的垂线，围成如图所示的矩形，A，B是所围成的矩形在x上方的两个顶点，若P，Q是椭圆C上两个动点，直线OP，OQ与椭圆的另外交点分别为P₁，Q₁，且直线OP，OQ的斜率之积等于直线OA，OB的斜率之积，试求四边形PQP₁Q₁的面积是否为定值，并说明理由．

3．若全集U={0，1，2，3，4，5，6}，A={1，3}，B={3，5}，则∁_U（A∪B）=（　　）

{0，2，4，6}