题目内容
11.化简${|{-0.01}|^2}-{({-\frac{5}{8}})^0}-{3^{{{log}_3}2}}+{({lg2})^2}+lg2lg5+lg5$的结果为-1.9999.分析 利用指数函数与对数函数的运算性质即可得出.
解答 解:原式=0.0001-1-2+lg2(lg2+lg5)+lg5
=0.0001-1-2+lg2+lg5
=0.0001-1-2+1
=-1.9999.
故答案为:-1.9999.
点评 本题考查了指数函数与对数函数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
3.若全集U={0,1,2,3,4,5,6},A={1,3},B={3,5},则∁U(A∪B)=( )
| A. | {2,4} | B. | {2,4,6} | C. | {0,2,4} | D. | {0,2,4,6} |
14.曲线的切线方程与直线6x-3y+1=0相互垂直,其中x的取值为非正数且曲线的方程为f(x)=2x3+x2-x(x2-1),则曲线的切线方程为( )
| A. | 2x+y+1=0 | B. | 2x+y-1=0 | C. | 2x-y-1=0 | D. | 2x-y+1=0 |
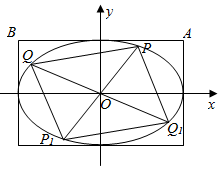 已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.
已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.