Question

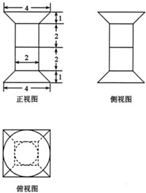一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V₁，V₂，V₃，V₄，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则V₁+V₂+V₃+V₄=（　　）

• A、

  48+13π

  3

• B、

  52+16π

  3

• C、

  42+13π

  3

• D、

  52+13π

  3

Answer 1

考点：由三视图求面积、体积

专题：计算题,空间位置关系与距离

分析：几何体是圆台、圆柱、正方体正四棱台的组与合体，根据三视图判断相关几何量的数据，利用圆台、圆柱、正方体、棱台的体积公式计算．

解答： 解：由三视图知：几何体是圆台、圆柱、正方体正四棱台的组合体，
圆台的上、下底面直径分别为4、2，高为1；
圆柱的底面直径为2，高为2；
正方体的棱长为2；
正四棱台的上、下底面边长分别为2、4，高为1．
∴几何体的体积V=

1

3

π×（2²+1²+2×1）×1+π×1²×2+2³+

1

3

×（2²+4²+2×4）×1=

7π

3

+2π+8+

28

3

=

52+13π

3

．
故选：D．

点评：本题考查了由三视图求几何体的体积，熟练掌握圆台、圆柱、正方体、棱台的体积公式是关键．