题目内容
在边长为3的等边三角形ABC中,点D、E分别在AB、AC上,且满足
=2
,
=
,则
•
=( )
| AD |
| DB |
| AE |
| 1 |
| 2 |
| EC |
| BE |
| CD |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量的共线定理、向量的三角形法则、数量积运算即可得出.
解答:
解:如图所示,
由等边三角形ABC的边长为3.
∴|
|=|
|=3,
•
=|
| |
|cos60°=3×3×
=
.
∵
=2
,
=
,
∴
=
+
=-
+
,
=
+
=-
+
.
∴
•
=(
-
)•(
-
)
=
•
-
2-
2
=
×
-
×32-
×32
=-
.
故选:B.

由等边三角形ABC的边长为3.
∴|
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| 1 |
| 2 |
| 9 |
| 2 |
∵
| AD |
| DB |
| AE |
| 1 |
| 2 |
| EC |
∴
| BE |
| BA |
| AE |
| AB |
| 1 |
| 3 |
| AC |
| CD |
| CA |
| AD |
| AC |
| 2 |
| 3 |
| AB |
∴
| BE |
| CD |
| 1 |
| 3 |
| AC |
| AB |
| 2 |
| 3 |
| AB |
| AC |
=
| 11 |
| 9 |
| AC |
| AB |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
=
| 11 |
| 9 |
| 9 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
=-
| 7 |
| 2 |
故选:B.
点评:本题考查了向量的共线定理、向量的三角形法则、数量积运算,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
抛物线C:x2=8y与直线y=2x-2相交于A,B两点,点P是抛物线C上不同A,B的一点,若直线PA,PB分别与直线y=2相交于点Q,R,O为坐标原点,则
•
的值是( )
| OR |
| OQ |
| A、20 | B、16 |
| C、12 | D、与点P位置有关的一个实数 |
若数列{an}满足:a1=1,a2=2,anan-2=an-1(n≥3),则a2012的值为( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、22012 |
已知F是抛物线y2=4x的焦点,准线与x轴的交点为M,点N在抛物线上,且|NF|=
|MN|,则∠FMN=( )
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、75° |
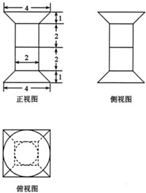 一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则V1+V2+V3+V4=( )
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则V1+V2+V3+V4=( )A、
| ||
B、
| ||
C、
| ||
D、
|