题目内容
过抛物线y2=-8x的焦点作一条直线与抛物线相交于A,B两点,它们到直线x=1的距离之和等于8,则这样的直线( )
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
考点:抛物线的简单性质
专题:
分析:过抛物线y2=-8x的焦点作一条直线与抛物线相交于A、B两点,先看直线AB斜率不存在时,求得它们到直线x=1的距离之和等于6,不符合题意;进而设直线AB为y=k(x+2)与抛物线方程联立消去y,进而根据韦达定理表示出A、B两点的横坐标之和,进而求得k.得出结论.
解答:
解:根据抛物线方程可知2p=8,p=2,开口向左,
∴抛物线的焦点坐标为(-2,0),
当直线AB斜率不存在时,直线AB方程为x=-2,则A,B到直线x=1的距离为3+3=6,不符合题意,
设直线AB的斜率为k,A(x1,y1),B(x2,y2)则直线方程为y=k(x+2),带入抛物线方程得k2x2+(4k2+8)x+4k2=0
∴x1+x2=-
,
而A,B到直线x=1的距离之和为-x1+(-x1)+2=2+
=8,
求得k=±2,
∴这样的直线有且仅有两条,
故选B.
∴抛物线的焦点坐标为(-2,0),
当直线AB斜率不存在时,直线AB方程为x=-2,则A,B到直线x=1的距离为3+3=6,不符合题意,
设直线AB的斜率为k,A(x1,y1),B(x2,y2)则直线方程为y=k(x+2),带入抛物线方程得k2x2+(4k2+8)x+4k2=0
∴x1+x2=-
| 4k2+8 |
| k2 |
而A,B到直线x=1的距离之和为-x1+(-x1)+2=2+
| 4k2+8 |
| k2 |
求得k=±2,
∴这样的直线有且仅有两条,
故选B.
点评:本题主要考查了直线与抛物线的位置关系.解题的关键是利用转换和化归思想,通过方程的解来解决解析几何的问题.

练习册系列答案
相关题目
抛物线C:x2=8y与直线y=2x-2相交于A,B两点,点P是抛物线C上不同A,B的一点,若直线PA,PB分别与直线y=2相交于点Q,R,O为坐标原点,则
•
的值是( )
| OR |
| OQ |
| A、20 | B、16 |
| C、12 | D、与点P位置有关的一个实数 |
函数f(x)=lg(x+1)+lg(x-1)的奇偶性是( )
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、既奇又偶函数 |
复数
(i为虚数单位),Z在复平面内所对应的点在( )
| i-1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
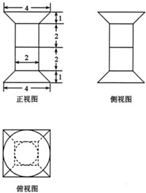 一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则V1+V2+V3+V4=( )
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则V1+V2+V3+V4=( )A、
| ||
B、
| ||
C、
| ||
D、
|
直线l与已知直线x+y-1=0垂直,则直线l的倾斜角为( )
| A、45° | B、135° |
| C、60° | D、30° |
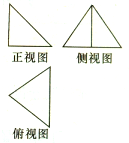 某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )
某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
| D、a3 |
 为了解高中生用电脑输入汉字的水平,随机抽取了部分学生进行每分钟输入汉字个数测试,如图是根据抽样测试后的数据绘制的频率分布直方图,其中每分钟输入汉字个数的范围是[50,150],样本数据分组为[50,70),[70,90),[90,110),[110,130),[130,150].已知样本中每分钟输入汉字个数小于90的人数是36,则样本中每分钟输入汉字个数不小于70个且小于130个的人数是( )
为了解高中生用电脑输入汉字的水平,随机抽取了部分学生进行每分钟输入汉字个数测试,如图是根据抽样测试后的数据绘制的频率分布直方图,其中每分钟输入汉字个数的范围是[50,150],样本数据分组为[50,70),[70,90),[90,110),[110,130),[130,150].已知样本中每分钟输入汉字个数小于90的人数是36,则样本中每分钟输入汉字个数不小于70个且小于130个的人数是( )