题目内容
已知函数f（x）=（
）x-log2x，若x0是函数y=f（x）的零点，则当0＜x＜x0时，函数f（x）（ ）
| 1 |
| 5 |
| A、恒为正值 | B、等于0 |
| C、恒为负值 | D、不大于0 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：将求函数f（x）的零点问题转化为求两个函数的交点问题，结合草图，问题容易求出．
解答：
解：令函数f（x）=(
)x-
=0，
∴(
)x=
，
令g（x）=(
)x，h（x）=
，
如图示：
，
∴当0＜x＜x0时，g（x）＞h（x），
∴当0＜x＜x0时，函数f（x）恒为正值．
故选：A．
| 1 |
| 5 |
| log | x 2 |
∴(
| 1 |
| 5 |
| log | x 2 |
令g（x）=(
| 1 |
| 5 |
| log | x 2 |
如图示：
，∴当0＜x＜x0时，g（x）＞h（x），
∴当0＜x＜x0时，函数f（x）恒为正值．
故选：A．
点评：本题考察了函数的零点问题，指数函数和对数函数的性质，渗透了数形结合思想，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若数列{an}满足：a1=1，a2=2，anan-2=an-1（n≥3），则a2012的值为（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
| D、22012 |
已知函数g（x）=x|a-x|+2x，若存在a∈[-2，3]，使得函数y=g（x）-at有三个零点，则实数t的取值范围是（ ）
A、（
| ||||
B、（2，
| ||||
C、（2，
| ||||
D、（2，
|
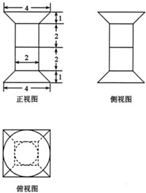一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V1，V2，V3，V4，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则V1+V2+V3+V4=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
若命题p1：y=log2014[（2-x）（2+x）]为偶函数；若命题p2：y=log2014
为奇函数，则下列命题为假命题的是（ ）
| 2-x |
| 2+x |
| A、p1∧p2 |
| B、p1∨￢p2 |
| C、p1∨p2 |
| D、p1∧￢p2 |
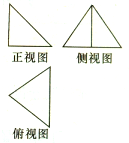某个几何体的三视图如图所示，其中侧视图是由一个边长为a的正三角形和底边上的高组成，俯视图是正三角形，则该几何体的体积为（ ）A、
| ||
B、
| ||
C、
| ||
| D、a3 |
设T（x）=|2x-1|，若不等式|a|T（x）≥|a+1|-|2a-1|对任意实数a≠0恒成立，则x的取值范围是（ ）
| A、（-∞，-1]∪[2，+∞） |
| B、（-∞，0]∪[1，+∞） |
| C、[0，1] |
| D、[-1，2] |
若某几何体的三视图如图所示（每个正方形的边长均为1），则该几何体的体积等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|