题目内容
已知数列{an}前项和为Sn,且满足Sn=2-an,n∈N+.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求a2+a4+…+a4n的和;
(Ⅲ)若记bn=Sn+2n-1,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求a2+a4+…+a4n的和;
(Ⅲ)若记bn=Sn+2n-1,求数列{bn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(I)利用递推式与等比数列的通项公式即可得出;
(II)利用等比数列的通项公式前n项和公式即可得出;
(III)利用等差数列与等比数列的通项公式前n项和公式即可得出.
(II)利用等比数列的通项公式前n项和公式即可得出;
(III)利用等差数列与等比数列的通项公式前n项和公式即可得出.
解答:
解:(I)∵Sn=2-an,n∈N+,
∴当n=1时,a1=2-a1,解得a1=1,
当n≥2时,Sn-1=2-an-1,∴an=an-1-an,即an=
an-1,
∴数列{an}是等比数列,首项为1,公比为
,
∴an=(
)n-1.
(II)由(I)可得:a2n=(
)2n-1,
∴
=
,
∴a2+a4+…+a4n=
=
(1-
);
(III)∵Sn=2-(
)n-1,
∴bn=Sn+2n-1=2-(
)n-1+2n-1=2n+1-(
)n-1,
∴数列{bn}的前n项和Tn=
-
=n2+2n-2+
.
∴当n=1时,a1=2-a1,解得a1=1,
当n≥2时,Sn-1=2-an-1,∴an=an-1-an,即an=
| 1 |
| 2 |
∴数列{an}是等比数列,首项为1,公比为
| 1 |
| 2 |
∴an=(
| 1 |
| 2 |
(II)由(I)可得:a2n=(
| 1 |
| 2 |
∴
| a4 |
| a2 |
| 1 |
| 4 |
∴a2+a4+…+a4n=
| ||||
1-
|
| 2 |
| 3 |
| 1 |
| 16n |
(III)∵Sn=2-(
| 1 |
| 2 |
∴bn=Sn+2n-1=2-(
| 1 |
| 2 |
| 1 |
| 2 |
∴数列{bn}的前n项和Tn=
| n(3+2n+1) |
| 2 |
1-
| ||
1-
|
| 1 |
| 2n-1 |
点评:本题考查了等差数列与等比数列的通项公式前n项和公式、递推式的应用,考查了变形能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若点P(a,b)与Q(b-1,a+1)(a≠b-1)关于直线l对称,则直线l的方程是( )
| A、x+y=0 |
| B、x-y=0 |
| C、x+y-1=0 |
| D、x-y+1=0 |
执行如图所示的程序框图,若m=4,则输出的结果为( )
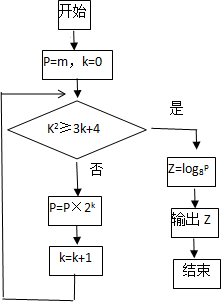

| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
已知函数f(x)=
,若函数g(x)=f(x)+x+a在R上恰有两个相异零点,则实数a的取值范围为( )
|
| A、[-1,+∞) |
| B、(-1,+∞) |
| C、(-∞,0) |
| D、(-∞,1] |

 如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.
如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.