题目内容
若直线a，b是异面直线，b与c也是异面直线，则a与c的位置关系是（ ）
| A、平行或异面 |
| B、相交，平行或异面 |
| C、异面或相交 |
| D、异面 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：以正方体为载体，利用空间中线线间的位置关系，能判断a与c的位置关系．
解答：
解：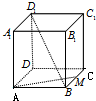
正方体ABCD-A1B1C1D1中，
①AD和A1B1是异面直线，AD和BB1是异面直线，
A1B1和BB1是相交线；
②AD和A1B1是异面直线，AD和D1C1是异面直线，
A1B1和D1C1是平行线；
③AD和A1B1是异面直线，AD和CC1是异面直线，
A1B1和CC1是异面线．
∴若直线a，b是异面直线，b与c也是异面直线，
则a与c的位置关系是相交，平行或异面．
故选：B．
正方体ABCD-A1B1C1D1中，①AD和A1B1是异面直线，AD和BB1是异面直线，
A1B1和BB1是相交线；
②AD和A1B1是异面直线，AD和D1C1是异面直线，
A1B1和D1C1是平行线；
③AD和A1B1是异面直线，AD和CC1是异面直线，
A1B1和CC1是异面线．
∴若直线a，b是异面直线，b与c也是异面直线，
则a与c的位置关系是相交，平行或异面．
故选：B．
点评：本题考查两直线位置关系的判断，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
如果函数f（x）=
+
-a在区间[-π，π]上有4个零点，那么实数a的取值范围是（ ）
| 1+sinx |
| 1-sinx |
A、（0，
| ||
| B、（1，2） | ||
C、（1，
| ||
D、（
|
已知函数y=sin2ωx+1（ω＞0）的最小正周期是
，则ω的值为（ ）
| π |
| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
一个正四棱锥的五个顶点都在半径为1的球面上，其中底面的四个顶点在该球的一个大圆上，则该正四棱锥的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式|x-3|+|x-2|≤3的解集为（ ）
| A、∅ |
| B、R |
| C、（-∞，1]∪[4，+∞） |
| D、[1，4] |
（理）已知
=a，且函数 f（x）=aebx-cx有大于0的极点值，则实数b的取值范围是（ ）
| lim |
| x→2 |
| x2+cx+2 |
| x-2 |
| A、（-∞，-3） | ||
| B、（-3，+∞） | ||
C、（-∞，-
| ||
D、（-
|
从装有4个红球和2个白球的口袋内任取3个球，那么互斥而不对立的两个事件是（ ）
| A、至少1个白球和都是红球 |
| B、恰有1个白球和都是红球 |
| C、至少1个白球和恰有1个红球 |
| D、至多1个白球和恰有1个红球 |
有600名同学参加夏令营，随机编号为000，001，…，599，现欲抽取50的样本，已知编号000～299的同学在第一营区，300～494的同学在第二营区，495-599的同学在第三营区，用系统抽样法，已知随机抽得的号码为002，则应从三个营区分别抽到的人数是（ ）
| A、26，16，8 |
| B、25，17，8 |
| C、25，16，9 |
| D、24，17，9 |