题目内容
已知函数f(x)=log2(4x+a),g(x)=x,设h(x)=f(x)-g(x)
(Ⅰ)若h(x)是偶函数,求a的值;
(Ⅱ)若关于x的方程h(x)=0有解,求a的取值范围.
(Ⅰ)若h(x)是偶函数,求a的值;
(Ⅱ)若关于x的方程h(x)=0有解,求a的取值范围.
考点:对数函数图象与性质的综合应用,函数奇偶性的判断
专题:函数的性质及应用
分析:(Ⅰ)根据h(x)是偶函数,得到h(-x)=h(x)成立,建立方程关系即可求a的值;
(Ⅱ)根据h(x)=0,将对数方程转化为指数方程,利用换元法,转化为二次函数,
(Ⅱ)根据h(x)=0,将对数方程转化为指数方程,利用换元法,转化为二次函数,
解答:
解:(I)∵f(x)=log2(4x+a),g(x)=x,
∴h(x)=f(x)-g(x)=log2(4x+a)-x,
∵h(x)是偶函数
∴h(-x)=h(x)成立,
即log2(4-x+a)+x=log2(4x+a)-x,恒成立,
整理得log2
=2x,
∴4x+a=(4-x+a)•4x=1+a•4x,
即a=1.
(II)由题意得:关于x的方程h(x)=0有解,
即log2(4x+a)=x有解,
即4x+a=2x有解,令2x=t,t>0,
∴a=-t2+t=-(t-
)2+
≤
,
即a的取值范围为(-∞,
].
∴h(x)=f(x)-g(x)=log2(4x+a)-x,
∵h(x)是偶函数
∴h(-x)=h(x)成立,
即log2(4-x+a)+x=log2(4x+a)-x,恒成立,
整理得log2
| 4x+a |
| 4-x+a |
∴4x+a=(4-x+a)•4x=1+a•4x,
即a=1.
(II)由题意得:关于x的方程h(x)=0有解,
即log2(4x+a)=x有解,
即4x+a=2x有解,令2x=t,t>0,
∴a=-t2+t=-(t-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
即a的取值范围为(-∞,
| 1 |
| 4 |
点评:本题主要考查函数奇偶性的应用,以及指数函数和对数函数的图象和性质,要求熟练掌握指数函数和对数函数的基本运算.

练习册系列答案
相关题目
若sin(α+
)=
,则cos2α=( )
| π |
| 2 |
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知函数f(x)=sinax(a>0)的最小正周期为π,为了得到g(x)=sin(ax+
)的图象,只要将y=f(x)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
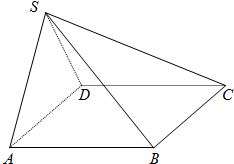 如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD. 某班同学进行了一次数学测试,将所得的数据整理后,画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,且第一小组的频数是5.
某班同学进行了一次数学测试,将所得的数据整理后,画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,且第一小组的频数是5. 已知正三棱柱ABC-A1B1C1中,AB=2,AA1=
已知正三棱柱ABC-A1B1C1中,AB=2,AA1=