题目内容
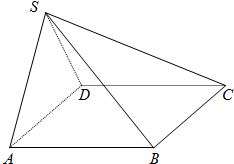 如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD.(1)求四棱锥S-ABCD的体积;
(2)在边CD上是否存在一点E,使得SB⊥AE?请说明理由.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)过点S作SF⊥AD,F为垂足,可得SF⊥底面ABCD,利用锥体的体积公式,即可求四棱锥S-ABCD的体积;
(2)在边CD上存在一点E,使得SB⊥AE,取边CD的中点E,连接AE、BF交于O,证明AE⊥BF,可得AE⊥平面SBF,即可证明SB⊥AE.
(2)在边CD上存在一点E,使得SB⊥AE,取边CD的中点E,连接AE、BF交于O,证明AE⊥BF,可得AE⊥平面SBF,即可证明SB⊥AE.
解答:
 解:(1)过点S作SF⊥AD,F为垂足.
解:(1)过点S作SF⊥AD,F为垂足.
因为侧面SAD垂直于底面ABCD,
所以SF⊥底面ABCD.
即SF为四棱锥S-ABCD的高.…(1分)
又侧面SAD为正三角形,且边长为a,
所以SF=
a.…(2分)
由此,VS-ABCD=
•AB•CD•SF=
×a×a×
a=
a3.…(4分)
所以四棱锥S-ABCD的体积为
a3.…(5分)
(2)在边CD上存在一点E,使得SB⊥AE.…(6分)
取边CD的中点E,连接AE、BF交于O.…(7分)
因为E、F分别为正方形ABCD的边CD、AD的中点,
所以△ADE和△BAF为全等的直角三角形,且∠AFB=∠DEA.…(8分)
而∠DEA+∠EAD=90°,所以∠AFB+∠EAD=90°,即∠AOF=90°.
所以AE⊥BF.…(10分)
又因为SF⊥底面ABCD,所以SF⊥AE,即AE⊥平面SBF,…(11分)
所以SB⊥AE.…(12分)
 解:(1)过点S作SF⊥AD,F为垂足.
解:(1)过点S作SF⊥AD,F为垂足.因为侧面SAD垂直于底面ABCD,
所以SF⊥底面ABCD.
即SF为四棱锥S-ABCD的高.…(1分)
又侧面SAD为正三角形,且边长为a,
所以SF=
| ||
| 2 |
由此,VS-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
所以四棱锥S-ABCD的体积为
| ||
| 6 |
(2)在边CD上存在一点E,使得SB⊥AE.…(6分)
取边CD的中点E,连接AE、BF交于O.…(7分)
因为E、F分别为正方形ABCD的边CD、AD的中点,
所以△ADE和△BAF为全等的直角三角形,且∠AFB=∠DEA.…(8分)
而∠DEA+∠EAD=90°,所以∠AFB+∠EAD=90°,即∠AOF=90°.
所以AE⊥BF.…(10分)
又因为SF⊥底面ABCD,所以SF⊥AE,即AE⊥平面SBF,…(11分)
所以SB⊥AE.…(12分)
点评:本题考查锥体体积的计算,考查线面垂直的判断,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
+
=1(x>0,y>0),则xy的最小值( )
| 5 |
| x |
| 3 |
| y |
| A、15 | B、6 | C、60 | D、1 |
| AB |
| BC |
| CD |
| DA |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图(1),在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,点M为CE上一点,且BM⊥平面ACE.
如图(1),在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,点M为CE上一点,且BM⊥平面ACE.