题目内容
下列说法正确的有 .
①函数y=log
(x2-2x-3)的单调增区间是(-∞,1);
②若集合A={y|y=x-1},B={y|y=x2-1},则A∩B={(0,-1),(1,0)};
③若函数f(x)在(-∞,0),[0,+∞)都是单调增函数,则f(x)在(-∞,+∞)上也是增函数;
④函数y=
是偶函数.
①函数y=log
| 1 |
| 2 |
②若集合A={y|y=x-1},B={y|y=x2-1},则A∩B={(0,-1),(1,0)};
③若函数f(x)在(-∞,0),[0,+∞)都是单调增函数,则f(x)在(-∞,+∞)上也是增函数;
④函数y=
| ||
| |x+1|+|x-2| |
考点:复合函数的单调性
专题:函数的性质及应用,简易逻辑
分析:求出原函数的单调增区间判断①;分别求解两个函数的值域取交集判断②;
由分段函数的单调性判断③;求出原函数的定义域,化简后直接由偶函数的定义判断④.
由分段函数的单调性判断③;求出原函数的定义域,化简后直接由偶函数的定义判断④.
解答:
解:①由x2-2x-3>0,得x<-1或x>3,
内函数t=x2-2x-3在(-∞,-1)上为减函数,
∴函数y=log
(x2-2x-3)的单调增区间是(-∞,-1).命题①错误;
②由A={y|y=x-1}=R,B={y|y=x2-1}={y|y≥-1},
∴A∩B={y|y≥-1}.命题②错误;
③若函数f(x)在(-∞,0),[0,+∞)都是单调增函数,f(x)在(-∞,+∞)上不一定是增函数.
命题③错误;
④由
,得-1≤x≤1.
∴函数y=
=
=
由f(-x)=
=
=f(x).
∴函数y=
是偶函数.命题④正确.
∴正确的命题是④.
故答案为:④.
内函数t=x2-2x-3在(-∞,-1)上为减函数,
∴函数y=log
| 1 |
| 2 |
②由A={y|y=x-1}=R,B={y|y=x2-1}={y|y≥-1},
∴A∩B={y|y≥-1}.命题②错误;
③若函数f(x)在(-∞,0),[0,+∞)都是单调增函数,f(x)在(-∞,+∞)上不一定是增函数.
命题③错误;
④由
|
∴函数y=
| ||
| |x+1|+|x-2| |
| ||
| x+1-x+2 |
| ||
| 3 |
由f(-x)=
| ||
| 3 |
| ||
| 3 |
∴函数y=
| ||
| |x+1|+|x-2| |
∴正确的命题是④.
故答案为:④.
点评:本题考查了命题的真假判断与应用,考查了基本初等函数的性质,解答此题的关键是对分段函数单调性的理解,是中档题.

练习册系列答案
相关题目
抛物线y2=-16x的焦点坐标为( )
| A、(0,-4) |
| B、(4,0) |
| C、(0,4) |
| D、(-4,0) |
函数f(x)=x3-3x2-9x+3,若函数g(x)=f(x)-m,在x∈[-2,5]上有3个零点,则m的取值范围为( )
| A、[1,8] |
| B、(-24,1] |
| C、[1,8) |
| D、(-24,8) |
已知△ABC中,a=2
,b=2
,A=60°,则B=( )
| 3 |
| 2 |
| A、450 |
| B、1350 |
| C、450或1350 |
| D、300或1500 |
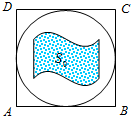 如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法:
如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法: