题目内容

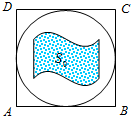如图，在边长为2的正方形ABCD中有一内切圆，某人为了用随机模拟的方法估计出该圆内阴影部分（旗帜）的面积S0，往正方形ABCD内随机撒了100粒品质相同 的豆子，结果有75粒落在圆内，有25粒落在阴影部分内，据此，有五种说法：
①估计S0=1；   
②估计S0=
π
2
；
③估计S0=
π
3
；  
④估计S0=
π
4
；
⑤估计S0=
4
3
．
那么以上说法中不正确的是
 
（填上所有不正确说法的序号）
考点：几何概型
专题：概率与统计
分析：先求出正方形的面积为4，设阴影部分的面积为S0，由概率的几何概型知阴影部分面积为正方形面积的
s0
2×2
=
25
75
或
s0
π
=
25
75
，由此可求阴影部分的面积．
解答： 解：解：设阴影部分的面积为S0，
由概率的几何概型知，则
s0
2×2
=
25
75
或
s0
π
=
25
75
，
解得S0=1或S0=
π
4
；
故答案为：②④⑤
点评：本题考查概率的性质和应用；每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概型．
练习册系列答案
相关题目
设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F，短轴上端点为B，连接BF并延长交椭圆于点A，连接AO并延长交椭圆于点D，过B、F、O三点的圆的圆心为C．
（1）若C的坐标为（-1，1），求椭圆方程和圆C的方程；
（2）若AD为圆C的切线，求椭圆的离心率．
已知直线ax+y-2=0与圆心为C的圆（x-2）2+（y-2）2=4相交于A，B两点，且△ABC为等边三角形，则实数a=
 
．
圆C：x2+y2-8x+4y+19=0关于直线x+y+1=0对称的圆的方程为
 
．
已知向量
m
=
3
sin2x
，
1
，
n
=
1
，
3+cos2x
，设函数f（x）=
m
•
n
．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）在△ABC中，a、b、c分别是角A、B、C的对边，若2
AC
•
BC
=
2
ab，c=2
2
，f（A）=4，求b．
已知f（x）=x2-4mx+1在[-2，+∞）为增函数，则m的取值范围是
 
．
下列说法正确的有
 
．
①函数y=log
1
2
(x2-2x-3)的单调增区间是（-∞，1）；
②若集合A={y|y=x-1}，B={y|y=x2-1}，则A∩B={（0，-1），（1，0）}；
③若函数f（x）在（-∞，0），[0，+∞）都是单调增函数，则f（x）在（-∞，+∞）上也是增函数；
④函数y=
1-x2
|x+1|+|x-2|
是偶函数．
下表是某单位在2013年1-5月份用水量（单位：百吨）的一组数据：
月份x12345
用水量y4.5432.51.8
（Ⅰ）若由线性回归方程得到的预测数据与实际检验数据的误差不超过0.05，视为“预测可靠”，通过公式得
?
b
=-0.7，那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠？说明理由；
（Ⅱ）从这5个月中任取2个月的用水量，求所取2个月的用水量之和小于7（单位：百吨）的概率．
参考公式：回归直线方程是：
?
a
=
.
y
-
?
b
.
x
，
?
y
=
?
b
x+
?
a
．
已知集合A={x|x2-x-2＜0}，B={x|y=lg
1-x
x+2
}，在区间（-3，3）上任取一实数x，则x∈A∩B的概率为（　　）
A、
1
3
B、
1
4
C、
1
8
D、
1
12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网