题目内容
已知x>a>0,求证:x3+13a2x>5ax2+9a3.
考点:不等式的证明,导数在最大值、最小值问题中的应用
专题:证明题,不等式的解法及应用
分析:方法一:构造函数f(x)=x3-5ax2+13a2x-9a3(x>0),求出导数,判断函数f(x)的单调性,运用单调性证明;
方法二:运用作差法证明,运用因式分解,将9a3拆成a3+13a3-5a3,提取公因式x-a,对括号里的化简配方,证到大于0即可.
方法二:运用作差法证明,运用因式分解,将9a3拆成a3+13a3-5a3,提取公因式x-a,对括号里的化简配方,证到大于0即可.
解答:
证法一:(函数单调性法)
设f(x)=x3-5ax2+13a2x-9a3(x>0),
则导数f'(x)=3x2-10ax+13a2,
=3(x-
a)2+
a2,
即对x>a>0时,f'(x)>0,
∴f(x)在x>0上是增函数,
∵x>a>0,∴f(x)>f(a),
∵f(a)=a3-5a3+13a3-9a3=0,
∴f(x)>0,原不等式成立.
证法二:(作差比较法)
∵x3+13a2x-5ax2-9a3=(x3-a3)+(13a2x-13a3)+(5a3-5ax2)
=(x-a)(x2+ax+a2)+13a2(x-a)-5a(x-a)(x+a)
=(x-a)[x2+ax+a2+13a2-5a(x+a)]
=(x-a)(x2-4ax+9a2)
=(x-a)[(x-2a)2+5a2],
又x>a>0,∴x-a>0,(x-2a)2+5a2>0,
∴x3+13a2x-5ax2-9a3>0,
∴x3+13a2x>5ax2+9a3.
设f(x)=x3-5ax2+13a2x-9a3(x>0),
则导数f'(x)=3x2-10ax+13a2,
=3(x-
| 5 |
| 3 |
| 14 |
| 3 |
即对x>a>0时,f'(x)>0,
∴f(x)在x>0上是增函数,
∵x>a>0,∴f(x)>f(a),
∵f(a)=a3-5a3+13a3-9a3=0,
∴f(x)>0,原不等式成立.
证法二:(作差比较法)
∵x3+13a2x-5ax2-9a3=(x3-a3)+(13a2x-13a3)+(5a3-5ax2)
=(x-a)(x2+ax+a2)+13a2(x-a)-5a(x-a)(x+a)
=(x-a)[x2+ax+a2+13a2-5a(x+a)]
=(x-a)(x2-4ax+9a2)
=(x-a)[(x-2a)2+5a2],
又x>a>0,∴x-a>0,(x-2a)2+5a2>0,
∴x3+13a2x-5ax2-9a3>0,
∴x3+13a2x>5ax2+9a3.
点评:本题考查不等式的证明方法,作差法证明是最基本的方法,运用函数的单调性证明往往简洁,但有时往往要运用导数这一重要工具,应认真领会.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
执行如图所示的程序框图,则输出的T为( )


| A、26 | B、57 | C、63 | D、120 |
设l,m,n为不同的直线,α,β为不同的平面,下列命题中正确的是( )
| A、若l∥α,m?α,则l∥m |
| B、若m∥n,n?α,则m∥α |
| C、若α不垂直于β,则α内不存在直线垂直于β |
| D、若α⊥β,l∥α,则l⊥β |
若集合A={x|2x-1>0},B={x||x|<1},则A∩B=( )
A、{
| ||
| B、(-1,1) | ||
C、[-1,
| ||
D、(
|
 已知直线x-2y+2=0经过椭圆C:
已知直线x-2y+2=0经过椭圆C: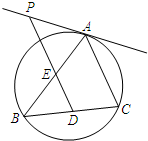 如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O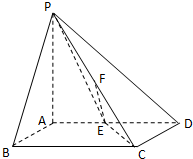 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.