题目内容
 已知椭圆C1:
已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ) 求椭圆C1和C2的方程;
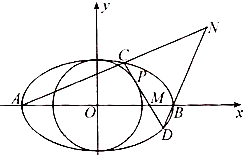
(Ⅱ) 如图,A,B分别为椭圆C1的左右顶点,P(x0,y0)为圆C2上的动点.过点P作圆C2的切线l,交椭圆C1与不同的两点C,D,且l与x轴的交点为M,直线AC与直线DB的交点为N.
(i) 求切线l的方程;
(ii) 问点M,N的横坐标之积是否为定值?若是定值,求出此定值;若不是定值,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ) 由题意,b=1,a=2,r=1,即可求椭圆C1和C2的方程;
(Ⅱ)(i)分类讨论,可得切线l的方程;
(ii) 由x0x+y0y=1,令y=0可得M的横坐标为xM=
,再求出xN=
=4x0,即可得出结论.
(Ⅱ)(i)分类讨论,可得切线l的方程;
(ii) 由x0x+y0y=1,令y=0可得M的横坐标为xM=
| 1 |
| x0 |
| 4x0x1x2-4x0(x1-x2)-2(x1+x2) |
| 2x0(x1+x2)-(x1-x2)-4 |
解答:
解:(Ⅰ)由题意,b=1,a=2,r=1,
∴椭圆C1的方程为
+y2=1;C2的方程为x2+y2=1;
(Ⅱ)(i) 显然x0≠0
①若y0=0,则切线l的方程为x=x0;
②若y0≠0,则切线l的方程为y-y0=-
(x-x0),即x0x+y0y=x02+y02,即x0x+y0y=1
由①②可知,切线l的方程为x0x+y0y=1;
(ii)由x0x+y0y=1,令y=0可得M的横坐标为xM=
,
x0x+y0y=1代入椭圆可得(y02+4x02)x2-8x0x+4-4y02=0,
设C(x1,y1),D(x2,y2),则
x1+x2=
,x1x2=
,
又直线AC的方程为y=
(x+2),直线BD的方程为y=
(x-2)
∴y1(x2-2)(x+2)=y1(x1+2)(x-2),
即(1-x0x1)(x2-2)(x+2)=(1-x0x2)(x1+2)(x-2),
∴xN=
=4x0,
∴xMxN=4.
∴M,N的横坐标之积为定值4.
∴椭圆C1的方程为
| x2 |
| 4 |
(Ⅱ)(i) 显然x0≠0
①若y0=0,则切线l的方程为x=x0;
②若y0≠0,则切线l的方程为y-y0=-
| x0 |
| y0 |
由①②可知,切线l的方程为x0x+y0y=1;
(ii)由x0x+y0y=1,令y=0可得M的横坐标为xM=
| 1 |
| x0 |
x0x+y0y=1代入椭圆可得(y02+4x02)x2-8x0x+4-4y02=0,
设C(x1,y1),D(x2,y2),则
x1+x2=
| 8x0 |
| y02+4x02 |
| 4-4y02 |
| y02+4x02 |
又直线AC的方程为y=
| y1 |
| x1+2 |
| y2 |
| x2-2 |
∴y1(x2-2)(x+2)=y1(x1+2)(x-2),
即(1-x0x1)(x2-2)(x+2)=(1-x0x2)(x1+2)(x-2),
∴xN=
| 4x0x1x2-4x0(x1-x2)-2(x1+x2) |
| 2x0(x1+x2)-(x1-x2)-4 |
∴xMxN=4.
∴M,N的横坐标之积为定值4.
点评:本题考查椭圆方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,难度大.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
如图是导函数y=f′(x)的图象,则下列命题错误的是( )
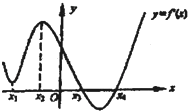

| A、导函数y=f′(x)在x1处有极小值 |
| B、导函数y=f′(x)在x2处有极大值 |
| C、导函数y=f(x)在x3处有极小值 |
| D、导函数y=f(x)在x4处有极小值 |
设-5<a<5,集合M={x∈N|2x-(a+5)x-10=0}.若M≠?,则满足条件的所有实数a的和等于( )
A、-
| ||
B、-
| ||
C、
| ||
| D、4 |