题目内容
如图是导函数y=f′(x)的图象,则下列命题错误的是( )
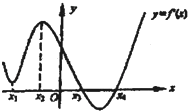

| A、导函数y=f′(x)在x1处有极小值 |
| B、导函数y=f′(x)在x2处有极大值 |
| C、导函数y=f(x)在x3处有极小值 |
| D、导函数y=f(x)在x4处有极小值 |
考点:函数在某点取得极值的条件
专题:导数的概念及应用
分析:逐个进行分析,分清研究对象是函数还是导函数.
解答:
解:根据题意,
对于选项A:
导函数y=f′(x)在x1处满足左减右增,
导函数y=f′(x)在x1处有极小值,
故选项A正确;
对于选项B:
导函数y=f′(x)在x1处满足左增右减,
导函数y=f′(x)在x1处有极大值,
故选项B正确;
对于选项C:
根据所给导函数y=f′(x)的图象,
使得f′(x)=0的x有x3和x4,
函数y=f(x)在x3处左侧为增函数,
其右侧为减函数,导函数y=f(x)在x3处有极大值,
故C错误,
对于选项D:
根据所给导函数y=f′(x)的图象,
使得f′(x)=0的x有x3和x4,
函数y=f(x)在x4处左侧为减函数,
其右侧为增函数,导函数y=f(x)在x4处有极小值,
故D正确,
故选:C.
对于选项A:
导函数y=f′(x)在x1处满足左减右增,
导函数y=f′(x)在x1处有极小值,
故选项A正确;
对于选项B:
导函数y=f′(x)在x1处满足左增右减,
导函数y=f′(x)在x1处有极大值,
故选项B正确;
对于选项C:
根据所给导函数y=f′(x)的图象,
使得f′(x)=0的x有x3和x4,
函数y=f(x)在x3处左侧为增函数,
其右侧为减函数,导函数y=f(x)在x3处有极大值,
故C错误,
对于选项D:
根据所给导函数y=f′(x)的图象,
使得f′(x)=0的x有x3和x4,
函数y=f(x)在x4处左侧为减函数,
其右侧为增函数,导函数y=f(x)在x4处有极小值,
故D正确,
故选:C.
点评:本题重点考查了函数的极值点和极值的概念和判断方法,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
i是虚数单位,计算
+
=( )
| 1-i |
| 1+i |
| 1+i |
| 1-i |
| A、-2i | B、0 | C、1 | D、2i |
已知集合A={x|x+3>0},则∁RA=( )
| A、(-∞,-3) |
| B、(-∞,-3] |
| C、(-3,+∞) |
| D、[-3,+∞) |
为了得到函数y=3cos(2x-
)的图象,只需要把函数y=3cos(2x)的图象上所有的点( )
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
我国的人口普查每十年进行一次,在第五次(2000年11月1日开始)人口普查时我国人口约为13亿,并发现我国人口的年平均增长率约为1%,如果按照这种速度增长,在我国开始第七次(2020年11月1日开始)普查时的人口数约为( )亿.
| A、13(1+20×1%) |
| B、13(1+19×1%) |
| C、13(1+1%)20 |
| D、13(1+1%)19 |
已知四面体的各条棱长均为2,则它的表面积是( )
A、
| ||
B、2
| ||
C、4
| ||
D、8
|
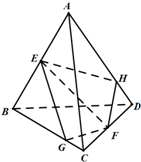 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )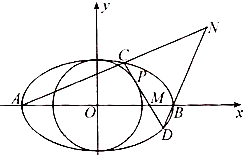 已知椭圆C1:
已知椭圆C1: