题目内容
已知数列{an}、{bn},其中,a1=
,数列{an}的前n项和Sn=n2an(n∈N*),数列{bn}满足b1=2,bn+1=2bn.
(1)求数列{an}、{bn}的通项公式;
(2)是否存在自然数m,使得对于任意n∈N*,n≥2,有1+
+
+…+
<
恒成立?若存在,求出m的最小值;
(3)若数列{cn}满足cn=
,求数列{cn}的前n项和Tn.
| 1 |
| 2 |
(1)求数列{an}、{bn}的通项公式;
(2)是否存在自然数m,使得对于任意n∈N*,n≥2,有1+
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| m-8 |
| 4 |
(3)若数列{cn}满足cn=
|
考点:数列与不等式的综合
专题:综合题,不等式的解法及应用
分析:(1)根据题设条件用累乘法能够求出数列{an}的通项公式.b1=2,bn+1=2bn可知{bn}是首项为2,公比为2的等比数列,由此能求出{bn}的通项公式.
(2)bn=2n.假设存在自然数m,使得对于任意n∈N*,n≥2,有1+
+
+…+
<
恒成立,由此能导出m的最小值.
(3)当n是奇数时,Tn=(
+
+…+
)+(b2+b4+…+bn-1),当n是偶数时,Tn=[
+
+…+
]+(b2+b4+…+bn),由此能推导出当n是偶数时,求数列{cn}的前n项和Tn.
(2)bn=2n.假设存在自然数m,使得对于任意n∈N*,n≥2,有1+
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| m-8 |
| 4 |
(3)当n是奇数时,Tn=(
| 1 |
| a1 |
| 1 |
| 3a3 |
| 1 |
| nan |
| 1 |
| a1 |
| 1 |
| 3a3 |
| 1 |
| (n-1)an-1 |
解答:
解:(1)因为Sn=n2an(n∈N*).
当n≥2时,Sn-1=(n-1)2an-1,
所以an=Sn-Sn-1=n2an-(n-1)2an-1
所以(n+1)an=(n-1)an-1,即
=
. …2分
又a1=
,
所以an=
•
•
…
•
•a1=
•
•
•…•
•
•
=
.…4分
当n=1时,上式成立,
因为b1=2,bn+1=2bn,所以{bn}是首项为2,公比为2的等比数列,
故bn=2n.…6分
(2)由(1)知bn=2n,则1+
+
+…+
=1+
+
+…+
=2-
.
假设存在自然数m,使得对于任意n∈N*,n≥2,有1+
+
+…+
<
恒成立,即2-
<
恒成立,由
≥2,解得m≥16.…9分
所以存在自然数m,使得对于任意n∈N*,n≥2,有1+
+
+…+
<
恒成立,
此时,m的最小值为16.…11分
(3)当n为奇数时,Tn=(
+
+…+
)+(b2+b4+…+bn-1)
=[2+4+…+(n+1)]+(22+24+…+2n-1)=
•
+
=
+
(2n-1-1);…13分
当n为偶数时,Tn=[
+
+…+
]+(b2+b4+…+bn)=(2+4+…+n)+(22+24+…+2n)
=
•
+
=
+
(2n-1).…15分
因此Tn=
. …16分.
当n≥2时,Sn-1=(n-1)2an-1,
所以an=Sn-Sn-1=n2an-(n-1)2an-1
所以(n+1)an=(n-1)an-1,即
| an |
| an-1 |
| n-1 |
| n+1 |
又a1=
| 1 |
| 2 |
所以an=
| an |
| an-1 |
| an-1 |
| an-2 |
| an-2 |
| an-3 |
| a3 |
| a2 |
| a2 |
| a1 |
| n-1 |
| n+1 |
| n-2 |
| n |
| n-3 |
| n-1 |
| 2 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n(n+1) |
当n=1时,上式成立,
因为b1=2,bn+1=2bn,所以{bn}是首项为2,公比为2的等比数列,
故bn=2n.…6分
(2)由(1)知bn=2n,则1+
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| 1 |
| 2n |
假设存在自然数m,使得对于任意n∈N*,n≥2,有1+
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| m-8 |
| 4 |
| 1 |
| 2n |
| m-8 |
| 4 |
| m-8 |
| 4 |
所以存在自然数m,使得对于任意n∈N*,n≥2,有1+
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| m-8 |
| 4 |
此时,m的最小值为16.…11分
(3)当n为奇数时,Tn=(
| 1 |
| a1 |
| 1 |
| 3a3 |
| 1 |
| nan |
=[2+4+…+(n+1)]+(22+24+…+2n-1)=
| 2+n+1 |
| 2 |
| n+1 |
| 2 |
4(1-4
| ||
| 1-4 |
| n2+4n+3 |
| 4 |
| 4 |
| 3 |
当n为偶数时,Tn=[
| 1 |
| a1 |
| 1 |
| 3a3 |
| 1 |
| (n-1)an-1 |
=
| 2+n |
| 2 |
| n |
| 2 |
4(1-4
| ||
| 1-4 |
| n2+2n |
| 4 |
| 4 |
| 3 |
因此Tn=
|
点评:本题是考查数列知识的综合运用题,难度较大,在解题时要认真审题,仔细作答.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
一批产品有A,B,C三种型号,数量分别是120件,80件,60件.为了解它们的质量是否存在差异,用分层抽样的方法抽取了一个容量为n的样本,其中从型号C的产品中抽取了3件,则n的值是( )
| A、9 | B、10 | C、12 | D、13 |
为了得到函数y=3cos(2x-
)的图象,只需要把函数y=3cos(2x)的图象上所有的点( )
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
设l,m是两条不同的直线,a是一个平面,则下列命题正确的是( )
| A、若l⊥m,m⊥a,则l∥a |
| B、若m⊥l,l?a,则m⊥a |
| C、若m∥l,l∥a,则m∥a |
| D、若l⊥a,m⊥a,则l∥m |
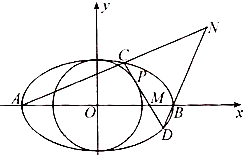 已知椭圆C1:
已知椭圆C1: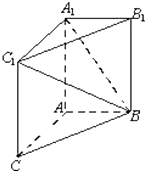 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3.