题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c.若△ABC的面积S=c2-(a-b)2,则tanC= .
考点:余弦定理
专题:解三角形
分析:利用三角形面积公式及余弦定理化简已知等式,整理即可求出tanC的值.
解答:
解:∵S△ABC=
absinC,cosC=
,即a2+b2-c2=2abcosC,
∴已知等式变形得:
absinC=-2abcosC+2ab,
∵ab≠0,∴
sinC=-2cosC+2,即sinC+4cosC=4,
与sin2C+cos2C=1,联立解得:cosC=
,sinC=
,
则tanC=
.
故答案为:
| 1 |
| 2 |
| a2+b2-c2 |
| 2ab |
∴已知等式变形得:
| 1 |
| 2 |
∵ab≠0,∴
| 1 |
| 2 |
与sin2C+cos2C=1,联立解得:cosC=
| 15 |
| 17 |
| 8 |
| 17 |
则tanC=
| 8 |
| 15 |
故答案为:
| 8 |
| 15 |
点评:此题考查了余弦定理,三角形面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )
第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )| A、甲、乙两人单场得分的最高分都是9分 |
| B、甲、乙两人单场得分的中位数相同 |
| C、甲运动员的得分更集中,发挥更稳定 |
| D、乙运动员的得分更集中,发挥更稳定. |
一批产品有A,B,C三种型号,数量分别是120件,80件,60件.为了解它们的质量是否存在差异,用分层抽样的方法抽取了一个容量为n的样本,其中从型号C的产品中抽取了3件,则n的值是( )
| A、9 | B、10 | C、12 | D、13 |
i是虚数单位,计算
+
=( )
| 1-i |
| 1+i |
| 1+i |
| 1-i |
| A、-2i | B、0 | C、1 | D、2i |
已知集合A={x|x+3>0},则∁RA=( )
| A、(-∞,-3) |
| B、(-∞,-3] |
| C、(-3,+∞) |
| D、[-3,+∞) |
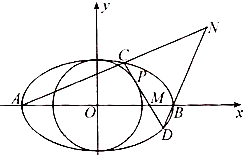 已知椭圆C1:
已知椭圆C1: