题目内容
一个以原点为圆心的圆与圆x2+y2+8x-4y=0关于直线l对称，则直线l的方程为 ．
考点：关于点、直线对称的圆的方程
专题：直线与圆
分析：求出圆的圆心坐标，然后求出中点坐标，求出对称轴的斜率，即可求解对称轴方程．
解答：
解：圆x2+y2+8x-4y=0的圆心坐标（-4，2），原点与圆心的中点坐标（-2，1），
对称轴的斜率为：-
=2，
直线l的方程为：y-2=2（x+2），即2x-y+5=0．
故答案为：2x-y+5=0；
对称轴的斜率为：-
| -2-0 |
| 1-0 |
直线l的方程为：y-2=2（x+2），即2x-y+5=0．
故答案为：2x-y+5=0；
点评：本题考查直线与圆的位置关系，对称轴方程的求法，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
已知集合A={x|x+3＞0}，则∁RA=（ ）
| A、（-∞，-3） |
| B、（-∞，-3] |
| C、（-3，+∞） |
| D、[-3，+∞） |
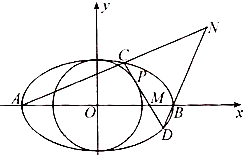已知椭圆C1：
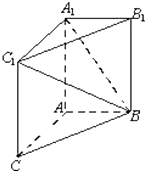如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形，AB⊥平面AA1C1C，AB=3．已知四面体的各条棱长均为2，则它的表面积是（ ）
A、
| ||
B、2
| ||
C、4
| ||
D、8
|