题目内容
16.现有12张不同的卡片,其中红色、黄色、蓝色、绿色卡片各3张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为189.分析 用间接法分析,先求出“从12张卡片中任取3张”的情况数目,再分析计算其中“同一种颜色”以及“有2张红色”的情况数目,用“从12张卡片中任取3张”的情况数目减去“同一种颜色”以及“有2张红色”的情况数目即可得答案.
解答 解:根据题意,不考虑限制条件,从12张卡片中任取3张有C123种情况,
其中如果取出的3张为同一种颜色,有4C33种情况,
如果取出的3张有2张红色的卡片,有C32C91种情况,
则满足条件的取法有C123-4C33-C32C91=189种;
故答案为:189.
点评 本题考查排列、组合的应用,解题时注意利用排除法分析,即先不考虑限制条件,求出全部的情况数目,再分析排出其中不符合条件的情况数目.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
7.某几何体的三视图如图所示,则该几何体的表面积为( )
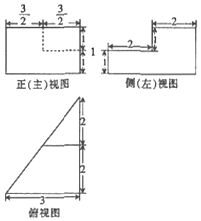

| A. | 30 | B. | 31.5 | C. | 33 | D. | 35.5 |
4.已知向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|=1$,($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,$({2\overrightarrow a+\overrightarrow b})⊥\overrightarrow b$,则向量$\overrightarrow a$,$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
6.已知函数f(x)=-x2+6x+a2-1,那么下列式子中正确的是( )
| A. | $f(\sqrt{2})<f(3)<f(4)$ | B. | $f(3)<f(\sqrt{2})<f(4)$ | C. | $f(\sqrt{2})<f(4)<f(3)$ | D. | $f(3)<f(4)<f(\sqrt{2})$ |
7.log39=( )
| A. | 5 | B. | 2 | C. | 3 | D. | 4 |
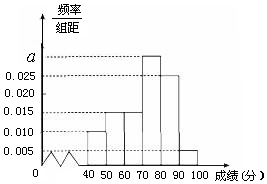 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: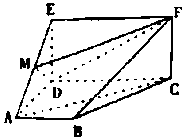 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.