题目内容
20. 如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )
如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )| A. | 直线AC与直线EC′所成角为45° | |
| B. | 点E到平面OCD′的距离为$\frac{1}{2}$ | |
| C. | 四面体O EA′B′在平面ABCD上的射影是面积为$\frac{1}{6}$的三角形 | |
| D. | 过点O,E,C的平面截正方体所得截面的面积为$\frac{\sqrt{6}}{2}$ |
分析 分别计算各选项的问题,得出结论.
解答 解:对于A,连结A′C′,A′E,C′E,则A′C′∥AC,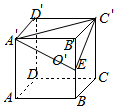
∴∠A′C′E为直线AC与直线EC′所成角,
在△A′C′E中,A′C′=$\sqrt{2}$,A′E=C′E=$\frac{\sqrt{5}}{2}$,
∴cos∠A′C′E=$\frac{2+\frac{5}{4}-\frac{5}{4}}{2×\sqrt{2}×\frac{\sqrt{5}}{2}}$=$\frac{\sqrt{10}}{5}$,
∴直线AC与直线EC′所成角的余弦值为$\frac{\sqrt{10}}{5}$,故A错误;
对于B,连结CD′,A′B,则O∈平面BCD′A′,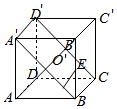
∴B′到平面BCD′A′的距离为$\frac{1}{2}$AB′=$\frac{\sqrt{2}}{2}$,
∴E到平面BCD′A′的距离为$\frac{\sqrt{2}}{4}$,故B错误;
对于C,O在底面ABCD的射影为正方形ABCD的中心,A′的射影为A,B′和E在底面的射影为B,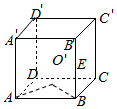
∴四面体O EA′B′在平面ABCD上的射影是面积为$\frac{1}{4}$的三角形,故C错误;
对于D,取DD′中点F,连结A′E,A′F,CE,CF,则菱形CEA′F是过O,C,E的平面与正方体的截面,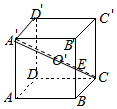
∵EF=$\sqrt{2}$,A′C=$\sqrt{3}$,∴截面面积S=$\frac{1}{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{6}}{2}$.故D正确.
故选D.
点评 本题考查了正方体的结构特征,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
2.我国古代数学名著《九章算术》有“米谷粒分”题:发仓募粮,所募粒中秕不百三则收之(不超过3%),现抽样取米一把,取得235粒米中夹秕n粒,若这批米合格,则n不超过( )
| A. | 6粒 | B. | 7粒 | C. | 8粒 | D. | 9粒 |
11.已知f(x)=x2+3x,若|x-a|≤1,则下列不等式一定成立的是( )
| A. | |f(x)-f(a)|≤3|a|+3 | B. | |f(x)-f(a)|≤2|a|+4 | C. | |f(x)-f(a)|≤|a|+5 | D. | |f(x)-f(a)|≤2(|a|+1)2 |
15.三棱锥P-ABC的三条侧棱两两垂直,且PA=PB=PC=1,则其外接球上的点到平面ABC的距离的最大值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
16.设向量$\overrightarrow{BA}$=(3,2),$\overrightarrow{BC}$=(3,-4),$\overrightarrow{AD}$=(0,2),则( )
| A. | $\overrightarrow{AB}∥\overrightarrow{BC}$ | B. | $\overrightarrow{AB}∥\overrightarrow{AD}$ | C. | $\overrightarrow{BC}∥\overrightarrow{AC}$ | D. | $\overrightarrow{AC}∥\overrightarrow{AD}$ |