题目内容
8.已知函数$f(x)=2sin({ωx+φ})+1({ω>0,|φ|<\frac{π}{2}}),f(α)=-1,f(β)=1$,若|α-β|的最小值为$\frac{3π}{4}$,且f(x)的图象关于点$({\frac{π}{4},1})$对称,则函数f(x)的单调递增区间是( )| A. | $[{-\frac{π}{2}+2kπ,π+2kπ}],k∈Z$ | B. | $[{-\frac{π}{2}+3kπ,π+3kπ}],k∈Z$ | ||
| C. | $[{π+2kπ,\frac{5π}{2}+2kπ}],k∈Z$ | D. | $[{π+3kπ,\frac{5π}{2}+3kπ}],k∈Z$ |
分析 由题意,f(α)=-1,f(β)=1,|α-β|的最小值为$\frac{3π}{4}$,可得周期T=4|α-β|=3π,可求出ω,图象关于点$({\frac{π}{4},1})$对称,带入求解φ.可得f(x)的解析式.将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间.
解答 解:由题意,函数$f(x)=2sin({ωx+φ})+1({ω>0,|φ|<\frac{π}{2}}),f(α)=-1,f(β)=1$,
α-β|的最小值为$\frac{3π}{4}$,
∴周期T=4|α-β|=3π,
ω=$\frac{2π}{T}$,即ω=$\frac{2}{3}$
∴f(x)=2sin($\frac{2}{3}x$+φ)+1
又∵图象关于点$({\frac{π}{4},1})$对称,
带入可得:sin($\frac{2}{3}×\frac{π}{4}+$φ)=0,即$\frac{π}{6}+$φ=kπ,k∈Z.
∵|φ|$<\frac{π}{2}$
∴φ=$-\frac{π}{6}$.
∴f(x)=2sin($\frac{2}{3}x$-$\frac{π}{6}$)+1
由$-\frac{π}{2}+2kπ≤$$\frac{2}{3}x$-$\frac{π}{6}$$≤\frac{π}{2}+2kπ$.
得:$-\frac{π}{2}+3kπ≤x≤π+3kπ$,k∈Z.
故选:B.
点评 本题主要考查对三角函数的计算能力和三角函数的图象和性质的运用,求解出三角函数解析式是解决本题的关键.属于基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
18. 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在GDP中的比重y关于年份代码x的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在GDP中的比重.
附注:回归直线方程$\widehaty=\widehata+\widehatbx$中的斜率和截距的最小二乘估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 第三产业比重y(%) | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
(2)建立第三产业在GDP中的比重y关于年份代码x的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在GDP中的比重.
附注:回归直线方程$\widehaty=\widehata+\widehatbx$中的斜率和截距的最小二乘估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
13.若复数z满足$(1+i)z=|{\sqrt{3}+i}|$,则在复平面内,$\overline z$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图所示的空间几何体中,底面四边形ABCD为正方形,AF⊥AB,AF∥BE,平面ABEF⊥平面ABCD,DF=$\sqrt{5}$,CE=2$\sqrt{2}$,BC=2.
如图所示的空间几何体中,底面四边形ABCD为正方形,AF⊥AB,AF∥BE,平面ABEF⊥平面ABCD,DF=$\sqrt{5}$,CE=2$\sqrt{2}$,BC=2.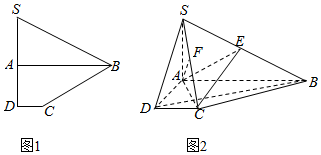 如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.
如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.