题目内容
18. 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 第三产业比重y(%) | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
(2)建立第三产业在GDP中的比重y关于年份代码x的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在GDP中的比重.
附注:回归直线方程$\widehaty=\widehata+\widehatbx$中的斜率和截距的最小二乘估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
分析 (1)根据所给数据,在所给坐标系中作出数据对应的散点图;
(2)求出回归系数,即可建立第三产业在GDP中的比重y关于年份代码x的回归方程;
(3)代入2017 年的年份代码x=7,得结论.
解答 解:(1)数据对应的散点图如图所示:
(2)$\overline x=3,\overline y=47.06$,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{15}{10}=1.5$,
$\widehata=\overline y-\widehatb\overline x=42.56$,
所以回归直线方程为$\widehaty=1.5x+42.56$.
(3)代入2017 年的年份代码x=7,得$\widehaty=1.5×7+42.56=53.06$,
所以按照当前的变化趋势,预计到2017年,我国第三产业在GDP中的比重将达到53.06%.
点评 本题考查独立性检验知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
9.已知双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,|F1F2|=2c.若双曲线M的右支上存在点P,使$\frac{a}{{sin∠P{F_1}{F_2}}}=\frac{3c}{{sin∠P{F_2}{F_1}}}$,则双曲线M的离心率的取值范围为( )
| A. | $(1,\frac{{2+\sqrt{7}}}{3})$ | B. | $(1,\frac{{2+\sqrt{7}}}{3}]$ | C. | (1,2) | D. | (1,2] |
3.已知点M(-1,0)和N(-1,0),若某直线上存在点p,使得|PM|+|PN|=4,则称该直线为“椭型直线”.现有下列直线:
①x-2y+6=0
②x-y=0
③2x-y+1=0
④x+y-3=0
其中是“椭型直线”的是( )
①x-2y+6=0
②x-y=0
③2x-y+1=0
④x+y-3=0
其中是“椭型直线”的是( )
| A. | ①③ | B. | ①② | C. | ②③ | D. | ③④ |
10.已知双曲线过点(2,3),渐进线方程为y=±$\sqrt{3}$x,则双曲线的标准方程是( )
| A. | $\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | $\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$ |
7.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{4}=1$过点(2,-1),则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
8.已知函数$f(x)=2sin({ωx+φ})+1({ω>0,|φ|<\frac{π}{2}}),f(α)=-1,f(β)=1$,若|α-β|的最小值为$\frac{3π}{4}$,且f(x)的图象关于点$({\frac{π}{4},1})$对称,则函数f(x)的单调递增区间是( )
| A. | $[{-\frac{π}{2}+2kπ,π+2kπ}],k∈Z$ | B. | $[{-\frac{π}{2}+3kπ,π+3kπ}],k∈Z$ | ||
| C. | $[{π+2kπ,\frac{5π}{2}+2kπ}],k∈Z$ | D. | $[{π+3kπ,\frac{5π}{2}+3kπ}],k∈Z$ |
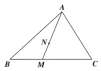 如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.
如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.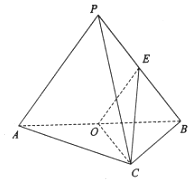 已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.
已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.