题目内容
19.已知函数$f(x)=\left\{\begin{array}{l}{2^{x-1}},x>1\\ tan\frac{πx}{3},x≤1\end{array}\right.$则$f(\frac{1}{f(2)})$=$\frac{\sqrt{3}}{3}$.分析 由已知得f(2)=22-1=2,从而$f(\frac{1}{f(2)})$=f($\frac{1}{2}$)=tan$\frac{π}{6}$,由此能求出结果.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}{2^{x-1}},x>1\\ tan\frac{πx}{3},x≤1\end{array}\right.$
∴f(2)=22-1=2,
$f(\frac{1}{f(2)})$=f($\frac{1}{2}$)=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{{\sqrt{3}}}{3}$.
点评 本题考查函数值的求法,考查推理论证能力、运算求解能力,考查化归与转化思想,函数与方程思想,是基础题.

练习册系列答案
相关题目
9.已知双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,|F1F2|=2c.若双曲线M的右支上存在点P,使$\frac{a}{{sin∠P{F_1}{F_2}}}=\frac{3c}{{sin∠P{F_2}{F_1}}}$,则双曲线M的离心率的取值范围为( )
| A. | $(1,\frac{{2+\sqrt{7}}}{3})$ | B. | $(1,\frac{{2+\sqrt{7}}}{3}]$ | C. | (1,2) | D. | (1,2] |
10.已知双曲线过点(2,3),渐进线方程为y=±$\sqrt{3}$x,则双曲线的标准方程是( )
| A. | $\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | $\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$ |
7.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{4}=1$过点(2,-1),则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
14.现阶段全国多地空气质量指数“爆表”.为探究车流量与PM2.5浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到12月某天7个不同时段车流量与PM2.5浓度的数据,如下表:
(1)根据上表中的数据,用最小二乘法求出y关于x的线性回归方程;
(2)规定当PM2.5浓度平均值在(0,50],空气质量等级为优;当PM2.5浓度平均值在(50,100],空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程:$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y=\widehatb\overline x$.
| 车流量x(万辆/小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5浓度y(微克/立方米) | 30 | 36 | 38 | 40 | 42 | 44 | 50 |
(2)规定当PM2.5浓度平均值在(0,50],空气质量等级为优;当PM2.5浓度平均值在(50,100],空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程:$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y=\widehatb\overline x$.
4.已知R为实数集,集合A={x|x2-2x≥0},B={x|x>1},则(∁RA)∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
8.已知函数$f(x)=2sin({ωx+φ})+1({ω>0,|φ|<\frac{π}{2}}),f(α)=-1,f(β)=1$,若|α-β|的最小值为$\frac{3π}{4}$,且f(x)的图象关于点$({\frac{π}{4},1})$对称,则函数f(x)的单调递增区间是( )
| A. | $[{-\frac{π}{2}+2kπ,π+2kπ}],k∈Z$ | B. | $[{-\frac{π}{2}+3kπ,π+3kπ}],k∈Z$ | ||
| C. | $[{π+2kπ,\frac{5π}{2}+2kπ}],k∈Z$ | D. | $[{π+3kπ,\frac{5π}{2}+3kπ}],k∈Z$ |
9.如图,在△ABC中,N、P分别是AC、BN的中点,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AP}$=( )
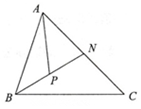

| A. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | B. | -$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C. | -$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ |